题目内容
若函数f(x)=
+
sin(2x-
)在[0,a]上的值域为[0,
],则实数a的取值( )
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
1+
| ||
| 2 |
A、[0,
| ||||
B、[
| ||||
| C、[0,π] | ||||
D、[
|
考点:正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:首先,根据所给条件,直接得到
≤2a-
≤
,然后,确定a的范围即可.
| π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
解答:
解:∵f(0)=0,且在[0,a]上的值域为[0,
],
∴
≤2a-
≤
,
∴
≤a≤
,
故选:B.
1+
| ||
| 2 |
∴
| π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
∴
| 3π |
| 8 |
| 3π |
| 4 |
故选:B.
点评:本题重点考查了三角函数的图象与性质,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
函数f(x)=ax3+bx2-3x在x=±1处取得极值,则f(x)的极大值是( )
| A、2 | B、4 | C、6 | D、8 |
直线x+y-1=0被圆x2+y2-2x-2y-6=0所截得弦的中点坐标是( )
| A、(1,0) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
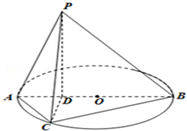 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=


