题目内容
设点A、B的坐标分别为(-a,0),(a,0),(a>0).直线AM,BM相交于点M,若它们的斜率之积是m(m≠0),求点M的轨迹方程,并指出是何种曲线.
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:设出M的坐标,求出直线的斜率,列出方程,化简即可得到轨迹方程,然后判断曲线即可.
解答:
解:设M(x,y)则kAM=
,kBM=
,(x≠-a)…(3分)
因为
•
=m(m≠0,x≠±a)…(6分)
所求轨迹方程为
-
=1(m≠0,x≠±a)…(9分)
当m<0时,轨迹为椭圆
当m>0时,轨迹为双曲线…(12分)
| y |
| x+a |
| y |
| x-a |
因为
| y |
| x+a |
| y |
| x-a |
所求轨迹方程为
| x2 |
| a2 |
| y2 |
| ma2 |
当m<0时,轨迹为椭圆
当m>0时,轨迹为双曲线…(12分)
点评:本题考查轨迹方程的求法,方程表示的曲线的判断,注意题目中隐含条件的求解,是易错点.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知F1、F2椭圆
+
=1左右焦点,P是椭圆是一点,|PF1|=5,则∠F2PF1的大小为( )
| x2 |
| 16 |
| 4y2 |
| 15 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)满足f(x)=f(
),且当x∈[
,1]时,f(x)=lnx,若当x∈[
,e]时,函数g(x)=f(x)-ax与x轴有两个相异交点,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| e |
| 1 |
| e |
| A、[-e,0) | ||
| B、[-e,0] | ||
C、[-
| ||
D、[-e,-
|
若函数f(x)=
+
sin(2x-
)在[0,a]上的值域为[0,
],则实数a的取值( )
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
1+
| ||
| 2 |
A、[0,
| ||||
B、[
| ||||
| C、[0,π] | ||||
D、[
|
若f(x)=x2+2xf′(1),则f′(0)=( )
| A、1 | B、2 | C、-4 | D、6 |
已知集合A={-1,0},则集合A的子集有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
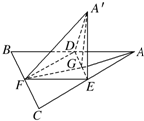 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是