题目内容
直线x+y-1=0被圆x2+y2-2x-2y-6=0所截得弦的中点坐标是( )
| A、(1,0) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
考点:直线与圆的位置关系
专题:直线与圆
分析:联立
,得2x2-2x-7=0,由此能求出直线x+y-1=0被圆x2+y2-2x-2y-6=0所截得弦的中点坐标.
|
解答:
解:联立
,
得2x2-2x-7=0,
设直线与圆的交点为A(x1,y1),B(x2,y2),
∴x1+x2=1,y1+y2=(1-x1)+(1-x2)=1,
∴直线x+y-1=0被圆x2+y2-2x-2y-6=0所截得弦的中点坐标是(
,
).
故选:D.
|
得2x2-2x-7=0,
设直线与圆的交点为A(x1,y1),B(x2,y2),
∴x1+x2=1,y1+y2=(1-x1)+(1-x2)=1,
∴直线x+y-1=0被圆x2+y2-2x-2y-6=0所截得弦的中点坐标是(
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查直线x+y-1=0被圆x2+y2-2x-2y-6=0所截得弦的中点坐标的求法,是基础题,解题时要认真审题,注意韦达定理的合理运用.

练习册系列答案
相关题目
函数f(x)=log2x-3sin
x的零点个数是( )
| π |
| 2 |
| A、3 | B、4 | C、5 | D、7 |
若函数f(x)=
+
sin(2x-
)在[0,a]上的值域为[0,
],则实数a的取值( )
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
1+
| ||
| 2 |
A、[0,
| ||||
B、[
| ||||
| C、[0,π] | ||||
D、[
|
若向量
=(1,t,2),
=(2,-1,2),且向量
与
垂直,则t等于( )
| a |
| b |
| a |
| b |
| A、-6 | ||
| B、6 | ||
| C、-2 | ||
D、-
|
已知f(x)=|2-x2|,若0<m<n时满足f(m)=f(n),则mn的取值范围为( )
| A、(0,2) | ||
| B、(0,2] | ||
| C、(0,4] | ||
D、(0,
|
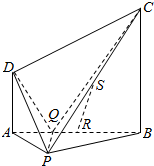 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.