题目内容
10.一拱桥为抛物线,当拱顶离水面2米时,水面宽4米.当水面下降2米后,水面宽为4$\sqrt{6}$米.分析 先建立直角坐标系,将A点代入抛物线方程求得m,得到抛物线方程,再把y=-4代入抛物线方程求得x0进而得到答案.
解答 解:如图建立直角坐标系,设抛物线方程为x2=my,
将A(2,-2)代入x2=my,
得m=-2
∴x2=-2y,代入B(x0,-4)得x0=2∴$\sqrt{2}$,
故水面宽为4$\sqrt{6}$m.
故答案为:4$\sqrt{6}$.
点评 本题主要考查抛物线的应用.考查了学生利用抛物线解决实际问题的能力,属于基础题.

练习册系列答案
相关题目
20.执行如图所示的程序框图,输出s的值为( )
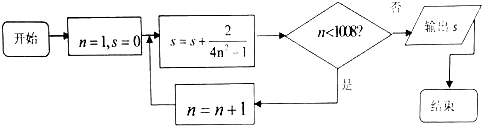

| A. | 1 | B. | $\frac{2018}{2019}$ | C. | $\frac{2018}{2017}$ | D. | $\frac{2016}{2017}$ |
2.函数f(x)=ax+b-1(其中0<a<1且0<b<1)的图象一定不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.三边长分别为4cm、5cm、6cm的三角形,其最大角的余弦值是( )
| A. | $-\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
 如图,某地区有四个单位分别位于矩形ABCD的四个顶点,且AB=2km,BC=4km,四个单位商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在变BC,CD上运动,若∠MAN=$\frac{π}{4}$,则△AMN面积的最小值为8$\sqrt{2}$-8km2.
如图,某地区有四个单位分别位于矩形ABCD的四个顶点,且AB=2km,BC=4km,四个单位商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在变BC,CD上运动,若∠MAN=$\frac{π}{4}$,则△AMN面积的最小值为8$\sqrt{2}$-8km2.