题目内容
18.已知函数f(x)=xlnx-ex+1(Ⅰ)求函数f(x)在点(1,f(1))处的切线方程;
(Ⅱ)证明:f(x)<sinx在(0,+∞)上恒成立.
分析 (Ⅰ)求出原函数的导函数,可得f(1)与f′(1)的值,代入直线方程的点斜式可得切线方程;
(Ⅱ)要证f(x)<sinx在(0,+∞)上恒成立,即xlnx-ex+1-sinx<0在(0,+∞)恒成立,也就是证xlnx<ex+sinx-1在(0,+∞)上恒成立,然后分0<x≤1与x>1证明,当0<x≤1时成立,当x>1时,令g(x)=ex+sinx-1-xlnx,然后两次求导即可证明f(x)<sinx在(0,+∞)上恒成立.
解答 (Ⅰ)解:f′(x)=lnx+1-ex,
f(1)=1-e,f′(1)=1-e,
故切线方程是:y-1+e=(1-e)(x-1),
即(1-e)x-y=0;
(Ⅱ)证明:要证f(x)<sinx在(0,+∞)上恒成立,
即xlnx-ex+1-sinx<0在(0,+∞)恒成立,也就是证xlnx<ex+sinx-1在(0,+∞)上恒成立,
当0<x≤1时,ex+sinx-1>0,xlnx≤0,
故xlnx<ex+sinx-1,也就是f(x)<sinx;
当x>1时,令g(x)=ex+sinx-1-xlnx,
g′(x)=ex+cosx-lnx-1,
令h(x)=g′(x)=ex+cosx-lnx-1,
h′(x)=${e}^{x}-\frac{1}{x}-sinx$>0,故h(x)在(1,+∞)上单调递增,
∴h(x)>h(1)=e+cos1-1>0,即g′(x)>0,则g(x)>g(1)=e+sin1-1>0,
即xlnx<ex+sinx-1,即f(x)<sinx,
综上所述,f(x)<sinx在(0,+∞)上恒成立.
点评 本题考查利用导数求函数在闭区间上的最值,考查利用导数研究过曲线上某点处的切线方程,利用两次求导判断函数的单调性是解答该题的关键,是压轴题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{4}$ | D. | $\frac{\sqrt{17}}{5}$ |
| A. | -$\frac{24}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{12}{25}$ | D. | $\frac{24}{25}$ |
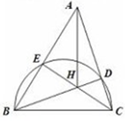 如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.
如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.