题目内容
20.执行如图所示的程序框图,输出s的值为( )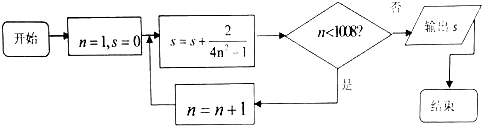
| A. | 1 | B. | $\frac{2018}{2019}$ | C. | $\frac{2018}{2017}$ | D. | $\frac{2016}{2017}$ |
分析 根据程序框图得到程序计算的是S=$\frac{2}{4×{1}^{2}-1}$+$\frac{2}{4×{2}^{2}-1}$+…+$\frac{2}{4×100{7}^{2}-1}$+$\frac{2}{4×100{8}^{2}-1}$,然后利用裂项法进行计算即可.
解答 解:∵$\frac{2}{4{n}^{2}-1}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$,
∴由程序框图可知该程序计算的是S=$\frac{2}{4×{1}^{2}-1}$+$\frac{2}{4×{2}^{2}-1}$+…+$\frac{2}{4×100{7}^{2}-1}$+$\frac{2}{4×100{8}^{2}-1}$
=$\frac{1}{1}$-$\frac{1}{3}$$+\frac{1}{3}$$-\frac{1}{5}$+…+$\frac{1}{2015}$-$\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$,
故选:D
点评 本题主要考查程序框图的应用,根据条件计算出满足条件的S,利用裂项法是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.某颜料公司生产A、B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨;生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨、160吨、200吨.如果A产品的利润为300元/吨,B产品的利润为200元/吨,则该颜料公司一天内可获得的最大利润为( )
| A. | 14000元 | B. | 16000元 | C. | 18000元 | D. | 20000元 |
9.设F是椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,P是C上的点,圆x2+y2=$\frac{{a}^{2}}{9}$与线段PF交于A、B两点,若A、B三等分线段PF,则C的离心率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{4}$ | D. | $\frac{\sqrt{17}}{5}$ |
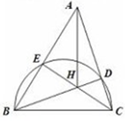 如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.
如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.