题目内容
已知点P（x，y）是椭圆
+
=1上的动点，用线性规划求2x+3y的取值范围．
| x2 |
| 9 |
| y2 |
| 4 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：目标函数z=2x+3y，P代表椭圆上动点，直线则代表目标函数，我们会发现，在直线移动的过程中，直线越往上移动，所代表的截距越大，那么目标函数值z也越大，反之则越小．由此我们可以得出在相切时，z分别取到最大最小值，即可得出结论．
解答：
解：目标函数z=2x+3y，P代表椭圆上动点，直线则代表目标函数，我们会发现，在直线移动的过程中，直线越往上移动，所代表的截距越大，那么目标函数值z也越大，反之则越小．
由此我们可以得出在相切时，z分别取到最大最小值，图象如下．
为了研究相切时的情况，我们可以联立椭圆和直线的方程，得到二次方程，8x2-4zx+z2-36=0
由于相切时方程有且仅有一解，所以令判别式△=0
得到16z2-32（z2-36）=0
即z2=72，此时z=±6
所以，zmax=6
，zmin=-6
因此目标函数2x+3y的取值范围是[-6
，6
]．
由此我们可以得出在相切时，z分别取到最大最小值，图象如下．
为了研究相切时的情况，我们可以联立椭圆和直线的方程，得到二次方程，8x2-4zx+z2-36=0
由于相切时方程有且仅有一解，所以令判别式△=0
得到16z2-32（z2-36）=0
即z2=72，此时z=±6
| 2 |
所以，zmax=6
| 2 |
| 2 |
因此目标函数2x+3y的取值范围是[-6
| 2 |
| 2 |
点评：本题考查椭圆方程，考查线性规划知识，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
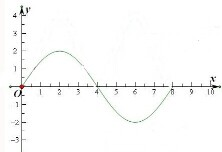已知函数f（x）=Asinωx（A＞0，ω＜0）的部分图象如图所示，则函数f（x）是（ ）| A、周期为8的偶函数 |
| B、周期为8的奇函数 |
| C、周期为8π的偶函数 |
| D、周期为8π的奇函数 |
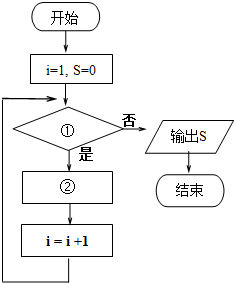已知等比数列{an}中，a1=1，公比q=2，计算数列{an}的前20项的和S，现已给出该算法的程序框图如图所示：