题目内容
9.已知数列{an}的前n项和是Sn,且Sn=2an-n(Ⅰ)求证:数列{an+1}为等比数列;并求数列{an}的通项公式an;
(Ⅱ)数列{bn}满足bn=$\frac{2n}{{a}_{n}+1}$,求数列{bn}的前n项和Tn;
(Ⅲ)若不等式(-1)nλ<Tn+$\frac{n}{{2}^{n-1}}$对一切n∈N*恒成立,求λ的取值范围.
分析 (Ⅰ)当n≥2时,Sn=2an-n,∴sn-1=2an-1-(n-1),两式相减,即可得数列{an+1}是首项和公比都是2的等比数列,
(Ⅱ)可得bn=$\frac{2n}{{a}_{n}+1}$=$\frac{n}{{2}^{n-1}}$,利用错位相减法求Tn
(Ⅲ)不等式(-1)nλ<Tn+$\frac{n}{{2}^{n-1}}$对一切n∈N*恒成立
?不等式(-1)nλ<4-$\frac{2}{{2}^{n-1}}$对一切n∈N*恒成立
由$f(n)=4-\frac{2}{{2}^{n-1}},n∈{N}^{+}$为递增函数,分n的奇偶讨论即可
解答 解:(Ⅰ)证明:当n=1时,s1=2a1-1=a1,∴a1+1=2≠0 …(1分)
当n≥2时,∵Sn=2an-n,∴sn-1=2an-1-(n-1),两式相减
∴an=2an-2an-1-1,∴an=2an-1+1,∴an+1=2(an-1+1)…(3分)
∴数列{an+1}是首项和公比都是2的等比数列,得an+1=2n⇒an=2n-1…(4分)
(Ⅱ)可得bn=$\frac{2n}{{a}_{n}+1}$=$\frac{n}{{2}^{n-1}}$,
Tn=$1×\frac{1}{{2}^{0}}+2×\frac{1}{{2}^{1}}+3×\frac{1}{{2}^{2}}+…+(n-1)\frac{1}{{2}^{n-2}}$+n×$\frac{1}{{2}^{n-1}}$
$\frac{1}{2}{T}_{n}$=1×$\frac{1}{{2}^{1}}+2×\frac{1}{{2}^{2}}$+…+(n-2)$\frac{1}{{2}^{n-2}}$+(n-1)$\frac{1}{{2}^{n-1}}$+n×$\frac{1}{{2}^{n}}$
,两式相减得$\frac{1}{2}{T}_{n}=\frac{1}{{2}^{0}}+\frac{1}{{2}^{1}}+…+\frac{1}{{2}^{n-1}}-n×\frac{1}{{2}^{n}}$=2-$\frac{n+2}{{2}^{n}}$
∴${T}_{n}=4-\frac{n+2}{{2}^{n-1}}$ …(8分)
(Ⅲ)不等式(-1)nλ<Tn+$\frac{n}{{2}^{n-1}}$对一切n∈N*恒成立
?不等式(-1)nλ<4-$\frac{2}{{2}^{n-1}}$对一切n∈N*恒成立
由$f(n)=4-\frac{2}{{2}^{n-1}},n∈{N}^{+}$为递增函数.…(9分)
若n为偶数,则λ<f(2)=3,∴λ<3 …(10分)
若n为奇数,则-λ<f(1)=2,∴-λ<2,λ>-2 …(11分)
∴-2<λ<3 …(12分)
点评 本题考查了数列的递推式、等比数列的判定、错位相减法求和、数列的单调性,属于中档题.

| A. | 两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱 | |
| B. | 若△ABC中,$\overrightarrow{AB}$•$\overrightarrow{BC}$<0,则△ABC是钝角三角形 | |
| C. | 函数f(x)=x+$\frac{4}{x-1}$(x>1)的最小值为5 | |
| D. | 若G2=ab,则G是a,b的等比中项 |
| A. | 150° | B. | 135° | C. | 300° | D. | 60° |
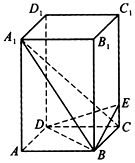 如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1
如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1 如图所示的几何体P-ABCD中,四边形ABCD为菱形,∠ABC=120°,AB=a,$PB=\sqrt{3}a$,PB⊥AB,平面ABCD⊥平面PAB,AC∩BD=O,E为PD的中点,G为平面PAB内任一点.
如图所示的几何体P-ABCD中,四边形ABCD为菱形,∠ABC=120°,AB=a,$PB=\sqrt{3}a$,PB⊥AB,平面ABCD⊥平面PAB,AC∩BD=O,E为PD的中点,G为平面PAB内任一点.