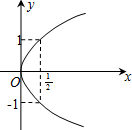题目内容
设a为实数,函数f(x)=3x2+(x-a)|x-a|
(1)若f(0)≥2,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥2的解集.
(1)若f(0)≥2,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥2的解集.
考点:函数的最值及其几何意义,其他不等式的解法
专题:分类讨论,不等式的解法及应用
分析:(1)分a≥0和a<0来讨论;
(2)去绝对值后,利用配方法求出函数最小值;
(3)转化为二次不等式,对方程的两根和a分别作比较,求出不等式的解集.
(2)去绝对值后,利用配方法求出函数最小值;
(3)转化为二次不等式,对方程的两根和a分别作比较,求出不等式的解集.
解答:
解:(1)f(0)≥2,-a|a|≥0,解得a≤0
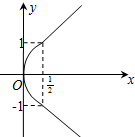
(2)f(x)=3x2+(x-a)|x-a|=
=
当x≥a时,f(x)=4(x-
)2+
,当x=
且a≤0时,f(x)min=
当x>a时,f(x)=2(x+
)2-
,当x=-
且a>0时,f(x)min=-
∴综上得:当a≤0时,f(x)的最小值为
,当a>0时,f(x)有最小值为-
.
(3)当x∈(a,+∞)时,f(x)=3x2+(x-a)2=4x2-2ax+a2,≠
∴h(x)≥2即4x2-2ax+a2-2≥0
△=(2a)2-16(a2-2)=32-12a2
①当△≤0时,即a2≥
即a∈(-∞,-
]∪[
,+∞)时,解集为(a,+∞);
②当△>0时,a∈(-
,
)时,
令4x2-2ax+a2-2=0,得x1=
,x2=
∴4x2-2ax+a2-2≥0,x≤x1 或x≥x2,
∵当a∈(-
,-
]时,x1≤a,解集为(a,
]∪[
,+∞);
当a∈(-
,0]时,x1<a,解集为[
,+∞);
当a=x2时,a=
,当a∈[
,
)时,a>x2,解集为(a,+∞);
当a∈(0,
)时,a<x2,解集为[
,+∞).
(2)f(x)=3x2+(x-a)|x-a|=
|
|
当x≥a时,f(x)=4(x-
| a |
| 4 |
| 3a2 |
| 4 |
| a |
| 4 |
| 3a2 |
| 4 |
当x>a时,f(x)=2(x+
| a |
| 2 |
| 3a2 |
| 2 |
| a |
| 2 |
| 3a2 |
| 2 |
∴综上得:当a≤0时,f(x)的最小值为
| 3a2 |
| 4 |
| 3a2 |
| 2 |
(3)当x∈(a,+∞)时,f(x)=3x2+(x-a)2=4x2-2ax+a2,≠
∴h(x)≥2即4x2-2ax+a2-2≥0
△=(2a)2-16(a2-2)=32-12a2
①当△≤0时,即a2≥
| 8 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
②当△>0时,a∈(-
2
| ||
| 3 |
2
| ||
| 3 |
令4x2-2ax+a2-2=0,得x1=
a-
| ||
| 4 |
a+
| ||
| 4 |
∴4x2-2ax+a2-2≥0,x≤x1 或x≥x2,
∵当a∈(-
2
| ||
| 3 |
| ||
| 3 |
a-
| ||
| 3 |
a+
| ||
| 4 |
当a∈(-
| ||
| 3 |
a+
| ||
| 4 |
当a=x2时,a=
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
当a∈(0,
| ||
| 3 |
a+
| ||
| 4 |
点评:本题考查了含绝对值不等式解法,运用了分类讨论、等价转换、配方法等思想方法,是一道综性较强的试题,属于难题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )
某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )A、2
| ||
B、4
| ||
| C、6 | ||
| D、8 |