题目内容
某旅游景点推出了自动购票机,为了解游客买票情况及所需时间等情况,随机收集了该景点100位游客的相关数据,如图所示:(将频率视为概率)
已知这50位顾客中一次购物量少于10件的顾客占80%.
(1)求x、y的值;
(2)求顾客一次购票所需时间X的分布列与数学期望.
(3)某游客去购票时,前面恰有2人在买票,求该游客购票前等候时间超过1.5分钟的概率.
| 一次购票 | 1张 | 2张 | 3张 | 4张 | 5张以上 |
| 游客人数 | x | 25 | 30 | y | 10 |
| 所需时间(秒/人) | 30 | 35 | 40 | 45 | 50 |
(1)求x、y的值;
(2)求顾客一次购票所需时间X的分布列与数学期望.
(3)某游客去购票时,前面恰有2人在买票,求该游客购票前等候时间超过1.5分钟的概率.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由已知30+y+10=55,由此能求出x、y的值.
(2)由已知得X的可能取值为30,35,40,45,50,分别求出相应的概率,由此能求出顾客一次购票所需时间X的分布列与数学期望.
(3)记A为事件“该游客购票前等候时间超过1.5分钟”,则P(A)=P(x1=45)×P(x2=50)+P(x1=50)×P(x2=45)+P(x1=50)×P(x2=50),由此能求出该游客购票前等候时间超过1.5分钟的概率.
(2)由已知得X的可能取值为30,35,40,45,50,分别求出相应的概率,由此能求出顾客一次购票所需时间X的分布列与数学期望.
(3)记A为事件“该游客购票前等候时间超过1.5分钟”,则P(A)=P(x1=45)×P(x2=50)+P(x1=50)×P(x2=45)+P(x1=50)×P(x2=50),由此能求出该游客购票前等候时间超过1.5分钟的概率.
解答:
解:(1)∵这100位游客中一次购票超过2张的游客占55%,
∴30+y+10=55,解得y=15,
∴x=100-25-30-15-10=20.
(2)由已知得X的可能取值为30,35,40,45,50,
P(X=30)=
=
,
P(X=35)=
=
,
P(X=40)=
=
,
P(X=45)=
=
,
P(X=50)=
=
,
∴X的分布列为:
∴EX=30×
+35×
+40×
+45×
+50×
=38.5.
(3)记A为事件“该游客购票前等候时间超过1.5分钟”,
则P(A)=P(x1=45)×P(x2=50)+P(x1=50)×P(x2=45)+P(x1=50)×P(x2=50)
=
×
+
×
+
×
=
.
∴30+y+10=55,解得y=15,
∴x=100-25-30-15-10=20.
(2)由已知得X的可能取值为30,35,40,45,50,
P(X=30)=
| 20 |
| 100 |
| 1 |
| 5 |
P(X=35)=
| 25 |
| 100 |
| 1 |
| 4 |
P(X=40)=
| 30 |
| 100 |
| 3 |
| 10 |
P(X=45)=
| 15 |
| 100 |
| 3 |
| 20 |
P(X=50)=
| 10 |
| 100 |
| 1 |
| 10 |
∴X的分布列为:
| X | 30 | 35 | 40 | 45 | 50 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 5 |
| 1 |
| 4 |
| 3 |
| 10 |
| 3 |
| 20 |
| 1 |
| 10 |
(3)记A为事件“该游客购票前等候时间超过1.5分钟”,
则P(A)=P(x1=45)×P(x2=50)+P(x1=50)×P(x2=45)+P(x1=50)×P(x2=50)
=
| 3 |
| 20 |
| 1 |
| 10 |
| 1 |
| 10 |
| 3 |
| 20 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 25 |
点评:本题考查相互独立事件概率、离散型随机变量的分布列及数学期望等基础知识,考查数据处理能力,考查化归与转化思想,是中档题.

练习册系列答案
相关题目
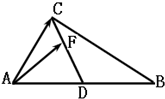 如图所示,在△ABC中,D为AB的中点,F在线段CD上,设
如图所示,在△ABC中,D为AB的中点,F在线段CD上,设| AB |
| a |
| AC |
| b |
| AF |
| a |
| b |
| 1 |
| x |
| 2 |
| y |
A、8+2
| ||
| B、8 | ||
| C、6 | ||
D、6+2
|
函数f(x)=2cosx(x∈[-π,π])的图象大致为( )
A、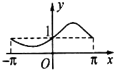 |
B、 |
C、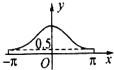 |
D、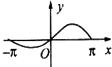 |