题目内容
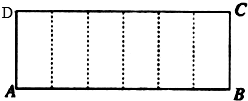
 某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )
某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )A、2
| ||
B、4
| ||
| C、6 | ||
| D、8 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图得该几何体是五面体,再由三视图求出五面体中有关集合元素的长度,代入梯形、等腰直角三角形的面积公式,再相加求出五面体的表面积.
解答:
解:由三视图得,该几何体是五面体,
如图所示, 底面是矩形ABCD,AB=2,AD=1,EF平行底面,EF=1,
底面是矩形ABCD,AB=2,AD=1,EF平行底面,EF=1,
过点E作EM⊥AB,垂足为M,则AM=
,则EM=1.
即DE=AE=
=
,
∴S梯形ABFE=S梯形CDEF=
×(1+2)×1=
,
S△ADE=S△BCF=
×1×
=
,S矩形ABCD=2×1=2,
∴该几何体表面积=2+2×
+2×
=6.
故选:C.
如图所示,
 底面是矩形ABCD,AB=2,AD=1,EF平行底面,EF=1,
底面是矩形ABCD,AB=2,AD=1,EF平行底面,EF=1,过点E作EM⊥AB,垂足为M,则AM=
| 1 |
| 2 |
即DE=AE=
| AM2+EM2 |
| ||
| 2 |
∴S梯形ABFE=S梯形CDEF=
| 1 |
| 2 |
| 3 |
| 2 |
S△ADE=S△BCF=
| 1 |
| 2 |
AE2-(
|
| 1 |
| 2 |
∴该几何体表面积=2+2×
| 1 |
| 2 |
| 3 |
| 2 |
故选:C.
点评:本题考查五面体的三视图,梯形、等腰直角三角形的面积计算公式,解题的关键是由三视图正确还原几何体,并求出几何体中几何元素的长度,考查了空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列式子中成立的是(假定各式均有意义)( )
| A、logax•logay=loga(x+y) | |||||
| B、(logax)n=nlogax | |||||
C、
| |||||
D、
|
 如图是某几何体的三视图,试求它的体积(单位:cm).
如图是某几何体的三视图,试求它的体积(单位:cm).