题目内容
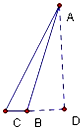如图，在△ABC中，AD⊥BC，D为垂足，AD在△ABC的外部，且BD：CD：AD=2：3：6，则tan∠BAC=（ ）| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点：余弦定理
专题：三角函数的求值
分析：根据BD：CD：AD=2：3：6，设出三边长，表示出BC，在直角三角形ACD中，利用勾股定理表示出AC，在直角三角形ABD中，利用勾股定理表示出AB，在三角形ABC中，利用余弦定理求出cos∠BAC的值，进而求出sin∠BAC的值，即可确定出tan∠BAC的值．
解答：
解：根据BD：CD：AD=2：3：6，得到BD=2x，CD=3x，AD=6x，
∴BC=CD-BD=3x-2x=x，
在Rt△ACD中，CD=3x，AD=6x，
根据勾股定理得：AC=
=3
x，
在Rt△ABD中，AD=6x，BD=2x，
根据勾股定理得：AB=
=2
x，
在△ABC中，利用余弦定理得：cos∠BAC=
=
=
，
∴sin∠BAC=
=
，
则tan∠BAC=
．
故选：B．
∴BC=CD-BD=3x-2x=x，
在Rt△ACD中，CD=3x，AD=6x，
根据勾股定理得：AC=
| CD2+AD2 |
| 5 |
在Rt△ABD中，AD=6x，BD=2x，
根据勾股定理得：AB=
| AD2+BD2 |
| 10 |
在△ABC中，利用余弦定理得：cos∠BAC=
| AB2+AC2-BC2 |
| 2AB•AC |
| 40x2+45x2-x2 | ||
60
|
7
| ||
| 10 |
∴sin∠BAC=
| 1-cos2∠BAC |
| ||
| 10 |
则tan∠BAC=
| 1 |
| 7 |
故选：B．
点评：此题考查了余弦定理，勾股定理，以及同角三角函数间的基本关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
设复数z1=1-i，z2=x+2i（x∈R），若
为实数，则x=（ ）
| z2 |
| z1 |
| A、-2 | B、-1 | C、1 | D、2 |
已知i为虚数单位，若
=y+2i，x，y∈R，则复数x+yi=（ ）
| x-i |
| i |
| A、2+i | B、-2-i |
| C、l-2i | D、1+2i |
若a=log3π，b=(
)0.3，c=log20.8，则（ ）
| 1 |
| 2 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、b＞c＞a |
设集合A={0，1，2，4，5，7}，集合B={1，3，6，8，9}，集合C={3，7，9}，则集合（A∩B）∪C等于（ ）
| A、{3，7，9} |
| B、{3，6，7，9} |
| C、{1，3，7，9} |
| D、{0，1，2，6，9} |
已知实数x、y满足
，则z=x+y的最小值等于（ ）
|
| A、0 | B、1 | C、4 | D、5 |
不等式
≥0的解集是（ ）
| 2-x |
| x-1 |
| A、（-∞，1）∪[2，+∞） |
| B、（-∞，1]∪[2，+∞） |
| C、[1，2] |
| D、（1，2] |
设{an}是一个等比数列，它的前3项的和为10，前6项的和为30，则它的前9项的和为（ ）
| A、50 | B、60 | C、70 | D、90 |
已知向量
=（1，cosα），
=（2，1）且
∥
，则锐角α的大小为（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|