题目内容
若a=log3π,b=(
)0.3,c=log20.8,则( )
| 1 |
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:根据对数函数的性质和指数幂的性质,分别求出a,b,c的范围,即可得到结论.
解答:
解:∵a=log3π>1,b=(
)0.3∈(0,1),c=log20.8<0,
∴a>1,0<b<1,c<0,
∴a>b>c,
故选:A.
| 1 |
| 2 |
∴a>1,0<b<1,c<0,
∴a>b>c,
故选:A.
点评:本题主要考查函数值的大小比较,利用对数函数和指数函数的性质是解决此类问题的关键.比较基础.

练习册系列答案
相关题目
下列函数中最小值为4的是( )
| A、y=4ex+e-x | ||||
B、y=x+
| ||||
C、y=
| ||||
| D、y=log3x+logx3(0<x<1) |
已知函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,则实数a的值为( )
| A、-1 | B、1 | C、±1 | D、-2 |
执行所示的程序框图,若输出的S是2047,则判断框内应填写( )


| A、n≤9? | B、n≤10? |
| C、n≥10? | D、n≥11? |
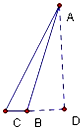 如图,在△ABC中,AD⊥BC,D为垂足,AD在△ABC的外部,且BD:CD:AD=2:3:6,则tan∠BAC=( )
如图,在△ABC中,AD⊥BC,D为垂足,AD在△ABC的外部,且BD:CD:AD=2:3:6,则tan∠BAC=( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
下列各式正确的是( )
A、
| |||||
B、a
| |||||
| C、3m=2?m=log32 | |||||
| D、lg(M+N)=lg(M)•lg(N),(M>0,N>0) |
已知sin(
+α)=
,则cos(
-α)等于( )
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|