题目内容
设集合A={0，1，2，4，5，7}，集合B={1，3，6，8，9}，集合C={3，7，9}，则集合（A∩B）∪C等于（ ）
| A、{3，7，9} |
| B、{3，6，7，9} |
| C、{1，3，7，9} |
| D、{0，1，2，6，9} |
考点：交、并、补集的混合运算
专题：集合
分析：由A与B，求出两集合的交集，再由C求出A与B交集与C的并集即可．
解答：
解：∵集合A={0，1，2，4，5，7}，集合B={1，3，6，8，9}，集合C={3，7，9}，
∴A∩B={1}，
则（A∩B）∪C={1，3，7，9}．
故选：C．
∴A∩B={1}，
则（A∩B）∪C={1，3，7，9}．
故选：C．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
复数z=
-（i-1）（i+1）的模是（ ）
| 1 |
| i |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
一个几何体的三视图如图所示，则该几何体的外接球的体积为（ ）
A、4
| ||
| B、12π | ||
C、2
| ||
D、4
|
已知函数f（x）=ax2+3x-2在点（2，f（2））处的切线斜率为7，则实数a的值为（ ）
| A、-1 | B、1 | C、±1 | D、-2 |
如果执行所示的程序框图，那么输出的S为（ ）
| A、96 | B、768 |
| C、1536 | D、768 |
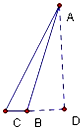如图，在△ABC中，AD⊥BC，D为垂足，AD在△ABC的外部，且BD：CD：AD=2：3：6，则tan∠BAC=（ ）| A、1 | ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示，则这个几何体的表面积等于（ ）
| A、72 | B、66 | C、60 | D、30 |
定义域为R的奇函数f（x），当x∈（-∞，0）时，f（x）+xf′（x）＜0恒成立，若a=3f（3），b=-f（-1），c=-2f（-2），则a，b，c的大小关系是（ ）
| A、a＞c＞b |
| B、c＞b＞a |
| C、c＞a＞b |
| D、a＞b＞c |
P为圆C1：x2+y2=9上任意一点，Q为圆C2：x2+y2=25上任意一点，PQ中点组成的区域为M，在C2内部任取一点，则该点落在区域M上的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|