题目内容
设{an}是一个等比数列，它的前3项的和为10，前6项的和为30，则它的前9项的和为（ ）
| A、50 | B、60 | C、70 | D、90 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据等比数列的前n项和的性质，建立方程关系即可得到结论．
解答：
解：∵等比数列前3项和为10，前6项和是30，
∴公比不等于-1，
则S3，S6-S3，S9-S6，也成等比数列，
即10，20，S9-30成等比数列，公比为2，
则S9-30=2×20=40，
解得S9=40+30=70，
故选：C
∴公比不等于-1，
则S3，S6-S3，S9-S6，也成等比数列，
即10，20，S9-30成等比数列，公比为2，
则S9-30=2×20=40，
解得S9=40+30=70，
故选：C
点评：本题主要考查等比数列的计算，利用等比数列前n项和的运算性质是解决本题的关键．
练习册系列答案
相关题目
下列函数中最小值为4的是（ ）
| A、y=4ex+e-x | ||||
B、y=x+
| ||||
C、y=
| ||||
| D、y=log3x+logx3（0＜x＜1） |
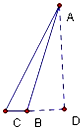如图，在△ABC中，AD⊥BC，D为垂足，AD在△ABC的外部，且BD：CD：AD=2：3：6，则tan∠BAC=（ ）| A、1 | ||
B、
| ||
C、
| ||
D、
|
下列各式正确的是（ ）
A、
| |||||
B、a
| |||||
| C、3m=2?m=log32 | |||||
| D、lg（M+N）=lg（M）•lg（N），（M＞0，N＞0） |
定义域为R的奇函数f（x），当x∈（-∞，0）时，f（x）+xf′（x）＜0恒成立，若a=3f（3），b=-f（-1），c=-2f（-2），则a，b，c的大小关系是（ ）
| A、a＞c＞b |
| B、c＞b＞a |
| C、c＞a＞b |
| D、a＞b＞c |
在△ABC中，若AD是边BC上的高，且AD=BC，则
+
的最大值是（ ）
| AC |
| AB |
| AB |
| AC |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
奇函数f（x）在区间[2，5]上为减函数，且有最大值7，则它在区间[-5，-2]上（ ）
| A、是减函数，有最大值-7 |
| B、是减函数，有最小值-7 |
| C、是增函数，有最大值-7 |
| D、是增函数，有最小值-7 |
已知sin（
+α）=
，则cos（
-α）等于（ ）
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|