题目内容
关于实数x的方程x+
=t-2|log2x|在区间[
,2]上有两个不同的实数根,则t∈ .
| 1 |
| x |
| 1 |
| 2 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:根据对数函数的性质,讨论x的取值将方程进行等价化简,然后将方程转化为函数,利用函数的图象即可得到结论.
解答:
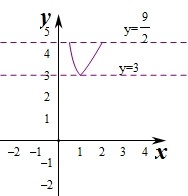 解:当1≤x≤2时,方程等价为x+
解:当1≤x≤2时,方程等价为x+
=t-2log2x=t-x,即t=2x+
,
当
≤x<1时,方程等价为x+
=t-2-log2x=t-2log2
=t-
,即t=x+
,
即t=
,
设f(x)=
.
当1≤x≤2时,函数f(x)=2x+
,则f'(x)=2-
=
>0,此时函数单调递增.∴3≤f(x)≤
.
当
≤x<1时,函数f(x)=x+
,则f'(x)=1-
=
<0,此时函数单调递减.∴3<f(x)≤
.
作出函数f(x)对应的图象如图:要使t=f(x)在区间[
,2]上有两个不同的实数根,
则满足3<t≤
,
即t∈(3,
],
故答案为:(3,
].
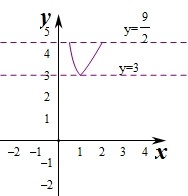 解:当1≤x≤2时,方程等价为x+
解:当1≤x≤2时,方程等价为x+| 1 |
| x |
| 1 |
| x |
当
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
即t=
|
设f(x)=
|
当1≤x≤2时,函数f(x)=2x+
| 1 |
| x |
| 1 |
| x2 |
| 2x2-1 |
| x2 |
| 9 |
| 2 |
当
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| x2 |
| x2-2 |
| x2 |
| 9 |
| 2 |
作出函数f(x)对应的图象如图:要使t=f(x)在区间[
| 1 |
| 2 |
则满足3<t≤
| 9 |
| 2 |
即t∈(3,
| 9 |
| 2 |
故答案为:(3,
| 9 |
| 2 |
点评:本题主要考查对数函数的基本运算,将函数进行等价化简是解决本题的关键,将方程转化为函数,利用数形结合是解决本题的基本思想.

练习册系列答案
相关题目
若直线mx-y+2=0与圆x2+y2=1只有一个交点,则实数m的值是( )
| A、±1 | ||
B、±
| ||
C、±
| ||
| D、±2 |
方程3x+3x-8=0必有一个根的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
 如图,DP⊥x轴,点M在DP的延长线上,且
如图,DP⊥x轴,点M在DP的延长线上,且