��Ŀ����
ij��˾�е���ÿ�����ٰ���280��ˮ���������֪�ù�˾��6��A�Ϳ�����8��B�Ϳ���������֪A�Ϳ���ÿ��ÿ����������Ϊ30�֣��ɱ���Ϊ0.9ǧԪ��B�Ϳ���ÿ��ÿ����������Ϊ40�֣��ɱ���Ϊ1ǧԪ��
��1��������ǹ�˾�ľ�����Ϊʹ��˾�����ijɱ�����С��ÿ��Ӧ�ɳ�A�Ϳ�����B�Ϳ�������������
��2���ڣ�1�������������ڣ���Ŀ�꺯��z=
�����ֵ����Сֵ��
��1��������ǹ�˾�ľ�����Ϊʹ��˾�����ijɱ�����С��ÿ��Ӧ�ɳ�A�Ϳ�����B�Ϳ�������������
��2���ڣ�1�������������ڣ���Ŀ�꺯��z=
| y |
| x+1 |
���㣺�����Թ滮��Ӧ��
ר�⣺���ν�Ϸ�,����ʽ�Ľⷨ��Ӧ��
��������1���ȸ������⣬�г�����ʽ�顢Ŀ�꺯������������������ͼ�����˾�����ijɱ�����С��ÿ��Ӧ�ɳ�A�Ϳ�����B�Ϳ�����
��2�����ã�1����������Ŀ�꺯���ļ��������������ڵĵ��루-1��0�����ߵ�б�ʣ�����Ŀ�꺯��z=
�����ֵ����Сֵ��
��2�����ã�1����������Ŀ�꺯���ļ��������������ڵĵ��루-1��0�����ߵ�б�ʣ�����Ŀ�꺯��z=
| y |
| x+1 |
���
�⣺��1���蹫˾ÿ���ɳ�A�Ϳ���x����B�Ϳ���y������˾�����ijɱ���ΪzǧԪ������1�֣�
�������⣬��
��Ŀ�꺯��z=0.9x+y������3�֣�
�����ò���ʽ���ʾ�Ŀ���������ͼ��
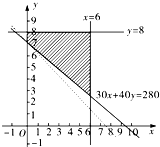 ����5�֣�
����5�֣�
����z=0.9x+y������Ϊy=-0.9x+z��������-0.9Ϊб�ʣ�zΪy���ϵĽؾ��ƽ��ֱ���壮
����������ƽ���ƶ�ֱ�ߣ���ֱ�߾����㣨0��7��ʱ��ֱ����y���ϵĽؾ���С����zȡ��Сֵ��Ϊ7����7�֣�
�𣺹�˾ÿ���ɳ�A�Ϳ���0����B�Ϳ���7��ʱ�������ijɱ�����ͣ�Ϊ7ǧԪ������8�֣�
��2�����ã�1����������Ŀ�꺯���ļ��������������ڵĵ��루-1��0�����ߵ�б�ʣ��ɵú����ڣ�0��8����ȡ���ֵ8���ڣ�6��3����ȡ��Сֵ
��
�������⣬��
|
�����ò���ʽ���ʾ�Ŀ���������ͼ��
 ����5�֣�
����5�֣�����z=0.9x+y������Ϊy=-0.9x+z��������-0.9Ϊб�ʣ�zΪy���ϵĽؾ��ƽ��ֱ���壮
����������ƽ���ƶ�ֱ�ߣ���ֱ�߾����㣨0��7��ʱ��ֱ����y���ϵĽؾ���С����zȡ��Сֵ��Ϊ7����7�֣�
�𣺹�˾ÿ���ɳ�A�Ϳ���0����B�Ϳ���7��ʱ�������ijɱ�����ͣ�Ϊ7ǧԪ������8�֣�
��2�����ã�1����������Ŀ�꺯���ļ��������������ڵĵ��루-1��0�����ߵ�б�ʣ��ɵú����ڣ�0��8����ȡ���ֵ8���ڣ�6��3����ȡ��Сֵ
| 3 |
| 7 |
���������⿼��������ѧ֪ʶ���ʵ�����⣬�������Թ滮֪ʶ�����ã�����ѧ���ļ��������������е��⣮

��ϰ��ϵ�д�
 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
�����Ŀ
��f(x)=
����f��2016�����ڣ�������
|
| A��0 |
| B��ln2 |
| C��1+e2 |
| D��1+ln2 |
����{an}��a1=1��a5=13��an+2+an=2an+1������{bn}��b2=6��b3=3��bn+2bn=b
����ֱ������ƽ���ڣ���֪����P1��a1��b1����P2��a2��b2����P3��a3��b3��������Pn��an��bn������������
+
+
+��+
��������������
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A����3015��8[��
| ||
B����3012��8[��
| ||
C����3015��8[��
| ||
D����3018��8[��
|
����f��x��=2x2-kx-8������[1��2]�ϲ���������ʵ��k��ȡֵ��ΧΪ��������
| A��[4��8] |
| B����-�ޣ�4]��[8��+�ޣ� |
| C����-�ޣ�4���ȣ�8��+�ޣ� |
| D����4��8�� |