题目内容
方程3x+3x-8=0必有一个根的区间是（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：利用根的存在性定理进行判断即可．
解答：
解：∵方程3x+3x-8=0，
∴设函数f（x）=3x+3x-8，
则函数f（x）=3x+3x-8在R上单调递增，
∵f（1）=3+3-8=-2＜0，f（2）=32+3×2-8=9+6-8=7＞0，
∴根据根的存在性定理可知函数f（x）在区间（1，2）内存在唯一的一个零点，
即方程3x+3x-8=0的根所在区间为（1，2），
故选：B．
∴设函数f（x）=3x+3x-8，
则函数f（x）=3x+3x-8在R上单调递增，
∵f（1）=3+3-8=-2＜0，f（2）=32+3×2-8=9+6-8=7＞0，
∴根据根的存在性定理可知函数f（x）在区间（1，2）内存在唯一的一个零点，
即方程3x+3x-8=0的根所在区间为（1，2），
故选：B．
点评：本题主要考查方程根的存在性的问题，利用方程和函数之间的关系，转化为函数，利用根的存在性定理判断函数零点所在的区间是解决本题的关键．
练习册系列答案
相关题目
已知△ABC三个顶点在同一个球面上，∠BAC=90°，AB=AC=2，若球心到平面ABC距离为1，则该球体积为（ ）
A、2
| ||
B、4
| ||
C、6
| ||
D、8
|
不等式组
的解在数轴上表示为（ ）
|
A、 |
B、 |
C、 |
D、 |
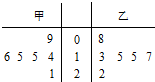甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，x1，x2分别表示甲乙两名运动员这项测试成绩的众数，s1，s2分别表示甲乙两名运动员这项测试成绩的标准差，则有（ ）| A、x1＞x2，s1＜s2 |
| B、x1=x2，s1＜s2 |
| C、x1=x2，s1=s2 |
| D、x1=x2，s1＞s2 |
过点M（x，0）向圆x2+y2-12y+27=0作两条切线，则两切线的最大夹角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若f(x)=
，则f（2016）等于（ ）
|
| A、0 |
| B、ln2 |
| C、1+e2 |
| D、1+ln2 |