题目内容
设A(1,0),B(0,1),直线l:y=ax,圆C:(x-a)2+y2=1.若圆C既与线段AB又与直线l有公共点,则实数a的取值范围是 .
考点:直线和圆的方程的应用
专题:直线与圆
分析:根据圆的圆心坐标和半径,首先分析得到使圆C:(x-a)2+y2=1与线段AB有公共点的a的范围,再由圆心到直线y=ax的距离小于等于圆的半径得到实数a的取值范围,取交集后得答案.
解答:
解:∵圆C:(x-a)2+y2=1的圆心C(a,0)在x轴上,且圆的半径等于1,
当圆心在A点左侧时,点A,B所在直线方程为x+y-1=0,
由圆心(a,0)到直线x+y-1=0的距离等于1,
得
=1,
即|a-1|=
,解得a=1-
或a=1+
(舍),
当圆心在A的右侧时,圆交线段AB于A时,a有最大值,此时a=2.
∴圆C:(x-a)2+y2=1与线段AB有公共点的a的范围是[1-
,2].
要使圆C:(x-a)2+y2=1与直线l:y=ax有公共点,则
≤1,
即a4≤a2+1,
∴a4-a2-1≤0,
解得:0≤a2≤
,
∴-
≤a≤
.
∴圆C既与线段AB又与直线l有公共点d的实数a的取值范围是[1-
,
].
故答案为:[1-
,
].
当圆心在A点左侧时,点A,B所在直线方程为x+y-1=0,
由圆心(a,0)到直线x+y-1=0的距离等于1,
得
| |a-1| | ||
|
即|a-1|=
| 2 |
| 2 |
| 2 |
当圆心在A的右侧时,圆交线段AB于A时,a有最大值,此时a=2.
∴圆C:(x-a)2+y2=1与线段AB有公共点的a的范围是[1-
| 2 |
要使圆C:(x-a)2+y2=1与直线l:y=ax有公共点,则
| |a2| | ||
|
即a4≤a2+1,
∴a4-a2-1≤0,
解得:0≤a2≤
1+
| ||
| 2 |
∴-
|
|
∴圆C既与线段AB又与直线l有公共点d的实数a的取值范围是[1-
| 2 |
|
故答案为:[1-
| 2 |
|
点评:本题考查了直线与圆的方程的应用,考查了分类讨论的数学思想方法,训练了利用圆心和直线的距离判断直线与圆的位置关系,属中档题.

练习册系列答案
相关题目
已知函数f(x)=cos2
x+
sin
xcos
x-2,则函数f(x)在[-1,1]上的单调增区间为( )
| π |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
A、[-
| ||||
B、[-1,
| ||||
C、[
| ||||
D、[-
|
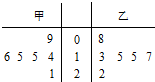 甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,x1,x2分别表示甲乙两名运动员这项测试成绩的众数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有( )
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,x1,x2分别表示甲乙两名运动员这项测试成绩的众数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有( )| A、x1>x2,s1<s2 |
| B、x1=x2,s1<s2 |
| C、x1=x2,s1=s2 |
| D、x1=x2,s1>s2 |
数列{an}中a1=1,a5=13,an+2+an=2an+1;数列{bn}中,b2=6,b3=3,bn+2bn=b
,在直角坐标平面内,已知点列P1(a1,b1),P2(a2,b2),P3(a3,b3),…,Pn(an,bn)…,则向量
+
+
+…+
的坐标为( )
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A、(3015,8[(
| ||
B、(3012,8[(
| ||
C、(3015,8[(
| ||
D、(3018,8[(
|