题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,短轴端点到焦点的距离为2.
(1)求椭圆C的方程;
(2)设点A,B是椭圆C上的任意两点,O是坐标原点,且OA⊥OB,
①求证:原点O到直线AB的距离为定值,并求出该定值;
②任取以椭圆C的长轴为直径的圆上一点P,求△PAB面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)设点A,B是椭圆C上的任意两点,O是坐标原点,且OA⊥OB,
①求证:原点O到直线AB的距离为定值,并求出该定值;
②任取以椭圆C的长轴为直径的圆上一点P,求△PAB面积的最大值.
考点:椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得:
=
,a=2,a2=b2+c2,解出即可得出;
(2)①当直线AB的斜率不存在时,直线AB的方程为x=±
,原点O到直线AB的距离为
是定值.当直线AB的斜率存在时,设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),与椭圆的方程联立可得根与系数的关系,由于
⊥
,可得
•
=0,可得m2=
.即可得出原点O到直线AB的距离=
.
②当直线AB的斜率不存在时,|AB|=
.
当直线AB的斜率存在时,利用弦长公式与基本不等式的性质可得|AB|=
≤
(k≠0).当k=0时,|AB|=
.可得|AB|的最大值为
.
由①可知:点P到直线AB的距离最大值为
+2,即可得出S△PAB最大值=
×
(
+2).
| c |
| a |
| ||
| 2 |
(2)①当直线AB的斜率不存在时,直线AB的方程为x=±
2
| ||
| 5 |
2
| ||
| 5 |
| OA |
| OB |
| OA |
| OB |
| 4+4k2 |
| 5 |
| |m| | ||
|
②当直线AB的斜率不存在时,|AB|=
4
| ||
| 5 |
当直线AB的斜率存在时,利用弦长公式与基本不等式的性质可得|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
| 5 |
4
| ||
| 5 |
| 5 |
由①可知:点P到直线AB的距离最大值为
2
| ||
| 5 |
| 1 |
| 2 |
| 5 |
2
| ||
| 5 |
解答:
(1)解:由题意可得:
=
,a=2,a2=b2+c2,
联立解得a=2,c=
,b=1.
∴椭圆C的方程为
+y2=1.
(2)①证明:当直线AB的斜率不存在时,直线AB的方程为x=±
,原点O到直线AB的距离为
是定值.
当直线AB的斜率存在时,设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
联立
,化为(1+4k2)x2+8kmx+4m2-4=0,
△=16(1+4k2-m2)>0,
x1+x2=
,x1x2=
,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
∵
⊥
,
∴
•
=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2=
=0,
∴m2=
.
∴原点O到直线AB的距离=
=
=
.
综上可得:原点O到直线AB的距离为定值
.
②解:当直线AB的斜率不存在时,|AB|=
.
当直线AB的斜率存在时,|AB|=
=
,
当k≠0时,|AB|=
≤
,当且仅当k=±
时取等号.
当k=0时,|AB|=
.
∴|AB|的最大值为
.
由①可知:点P到直线AB的距离最大值为
+2,
∴S△PAB最大值=
×
(
+2)=1+
.
| c |
| a |
| ||
| 2 |
联立解得a=2,c=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
(2)①证明:当直线AB的斜率不存在时,直线AB的方程为x=±
2
| ||
| 5 |
2
| ||
| 5 |
当直线AB的斜率存在时,设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
联立
|
△=16(1+4k2-m2)>0,
x1+x2=
| -8km |
| 1+4k2 |
| 4m2-4 |
| 1+4k2 |
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
∵
| OA |
| OB |
∴
| OA |
| OB |
| 5m2-4-4k2 |
| 1+4k2 |
∴m2=
| 4+4k2 |
| 5 |
∴原点O到直线AB的距离=
| |m| | ||
|
| ||||
|
2
| ||
| 5 |
综上可得:原点O到直线AB的距离为定值
2
| ||
| 5 |
②解:当直线AB的斜率不存在时,|AB|=
4
| ||
| 5 |
当直线AB的斜率存在时,|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
| 4 | ||
|
1+
|
当k≠0时,|AB|=
| 4 | ||
|
1+
|
| 5 |
| 1 |
| 2 |
当k=0时,|AB|=
4
| ||
| 5 |
∴|AB|的最大值为
| 5 |
由①可知:点P到直线AB的距离最大值为
2
| ||
| 5 |
∴S△PAB最大值=
| 1 |
| 2 |
| 5 |
2
| ||
| 5 |
| 5 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、向量垂直与数量积的关系、三角形的面积计算公式、基本不等式的性质,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知a∈R,条件p:函数f(x)=(a2-2a-2)x是增函数,条件q:函数g(x)=xa+2在区间(0,+∞)上是减函数,那么p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设a,b∈R,则“(a-b)a2<0”是“a<b”的( )条件.
| A、充要 |
| B、充分而不必要 |
| C、必要而不充分 |
| D、既不充分也不必要 |
已知函数f(x)=x+
+m(p≠0)是奇函数,
(1)求m的值;
(2)若p=-1,用定义证明函数f(x)=x-
在区间(0,+∞)上的单调性.
(3)若p<0,当x∈[1,3]时,求f(x)的最值.
| p |
| x |
(1)求m的值;
(2)若p=-1,用定义证明函数f(x)=x-
| 1 |
| x |
(3)若p<0,当x∈[1,3]时,求f(x)的最值.
若△ABC的三个内角A、B、C成等差数列,则cos(A+C)=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
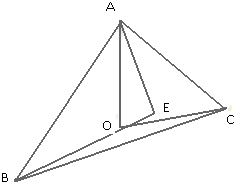 如图,O为△ABC的外心,E为三角形内一点,满足
如图,O为△ABC的外心,E为三角形内一点,满足