题目内容

设a，b∈R，则“（a-b）a2＜0”是“a＜b”的（　　）条件．
A、充要
B、充分而不必要
C、必要而不充分
D、既不充分也不必要
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质，结合充分条件和必要条件的定义即可得到结论．
解答： 解：若（a-b）a2＜0，则a≠0，∴a-b＜0，即a＜b成立，
若a=0，b=1，满足a＜b，但（a-b）a2＜0不成立，
即“（a-b）a2＜0”是“a＜b”的充分不必要条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，根据不等式的关系是解决本题的关键．
练习册系列答案
相关题目
已知向量
a
=(sinx，
3
2
)，
b
=(
1
2
，cosx)，f（x）=
a
•
b
．
（1）求函数y=f（x）的解析式；
（2）求函数y=f（x）的单调递增区间．
某工厂从2001年开始，近八年以来生产某种产品的情况是：前四年年产量的增长速度越来越快，后四年年产量的增长速度保持不变，则该厂这种产品的产量与时间的函数图象可能是（　　）
A、
B、
C、
D、
已知命题p：
x+1
x-1
＜0，命题q：（x-a）（x-3）＞0，若p是q的充分不必要条件，则实数a 的取值范围是（　　）
A、[1，3]
B、[1，3]
C、[1，+∞）
D、[3，+∞）
函数y=Asin（ωx+φ）图象的一部分如图所示，则此函数的解析式可以写成（　　）
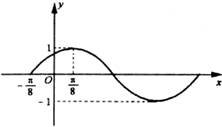
A、y=sin（2x+
π
4
）
B、y=sin（x+
π
8
）
C、y=sin（2x+
π
8
）
D、y=sin（2x-
π
4
）
设函数f（x）=cosxcos（x-θ）-
1
2
cosθ，θ∈（0，π），已知当x=
π
3
取得最大值为
1
2
．
（1）求θ的值；
（2）设g（x）=2f（
3
2
x），求g（x）在[0，
π
3
]上的最小值．
程序框图如图所示，则输出S的值为（　　）
A、15B、21C、22D、28
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，短轴端点到焦点的距离为2．
（1）求椭圆C的方程；
（2）设点A，B是椭圆C上的任意两点，O是坐标原点，且OA⊥OB，
①求证：原点O到直线AB的距离为定值，并求出该定值；
②任取以椭圆C的长轴为直径的圆上一点P，求△PAB面积的最大值．
已知函数f（x）=ln（ax）+（b-2）x（a，b是常数），此函数对应的曲线y=f（x）在点（1，-1）处的切线与直线x轴平行．
（Ⅰ）求a，b的值，并求f（x）的最大值；
（Ⅱ）设m≠0，函数g（x）=
1
3
mx3-mx，x∈（1，2），总存在x1∈（1，2），x2∈（1，2），使f（x1）-g（x2）=0，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网