题目内容
如图,在△ABC中,DE∥BC,EF∥CD,且AB=2,AD=
,则AF= .
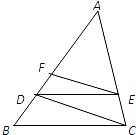
| 2 |

考点:相似三角形的性质
专题:立体几何
分析:由已知得△ADE∽△ABC,△AFE∽△ADC,从而
=
=
,由此能求出AF=
=
=1.
| AD |
| AB |
| AE |
| AC |
| AF |
| AD |
| AD2 |
| AB |
(
| ||
| 2 |
解答:
解:∵在△ABC中,DE∥BC,EF∥CD,
且AB=2,AD=
,
∴△ADE∽△ABC,△AFE∽△ADC,
∴
=
=
,
∴AF=
=
=1.
故答案为:1.
且AB=2,AD=
| 2 |
∴△ADE∽△ABC,△AFE∽△ADC,
∴
| AD |
| AB |
| AE |
| AC |
| AF |
| AD |
∴AF=
| AD2 |
| AB |
(
| ||
| 2 |
故答案为:1.
点评:本题考查三角形中线段长的求法,是基础题,解题时要注意相似三角形的性质的合理运用.

练习册系列答案
相关题目
函数y=Asin(ωx+φ)图象的一部分如图所示,则此函数的解析式可以写成( )
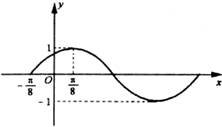

A、y=sin(2x+
| ||
B、y=sin(x+
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
程序框图如图所示,则输出S的值为( )


| A、15 | B、21 | C、22 | D、28 |
已知等差数列{an}中,a5+a6=7,则S10=( )
| A、35 | B、70 | C、42 | D、49 |
若函数y=f(x)的定义域为[-3,5],则函数g(x)=f(x+1)+f(x-2)的定义域是( )
| A、[-2,3] |
| B、[-1,3] |
| C、[-1,4] |
| D、[-3,5] |