题目内容
化简：
+
+
+
+
．
| 1 |
| a(a+1) |
| 1 |
| (a+1)(a+2) |
| 1 |
| (a+2)(a+3) |
| 1 |
| (a+3)(a+4) |
| 1 |
| (a+4)(a+5) |
考点：数列的求和
专题：等差数列与等比数列
分析：利用裂项求和法求解．
解答：
解：
+
+
+
+
=
-
+
-
+
-
+
-
+
-
=
-
．
| 1 |
| a(a+1) |
| 1 |
| (a+1)(a+2) |
| 1 |
| (a+2)(a+3) |
| 1 |
| (a+3)(a+4) |
| 1 |
| (a+4)(a+5) |
=
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 1 |
| a+3 |
| 1 |
| a+4 |
| 1 |
| a+4 |
| 1 |
| a+5 |
=
| 1 |
| a |
| 1 |
| a+5 |
点评：本题考查数列的前n项和的求法，是中档题，解题时要认真审题，注意裂项求和法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
下列命题中，正确的是（ ）
| A、若三条直线两两平行，则这三条直线必共面 |
| B、互不平行的两条直线是异面直线 |
| C、分别位于两个不同平面内的两条直线是异面直线 |
| D、不同在任何一个平面内的两条直线是异面直线 |
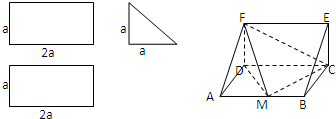一个多面体的三视图和直观图如图所示，其中正视图和俯视图均为矩形，侧视图为直角三角形，M是AB的中点．
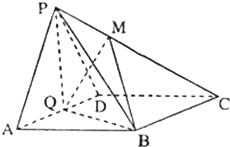如图，四棱锥P-ABCD中，四边形ABCD为平行四边形，面PAD⊥平面ABCD，PA=PD，Q为AD的中点，且QB⊥AD．