题目内容
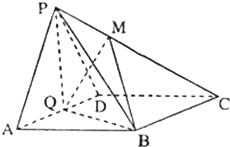如图，四棱锥P-ABCD中，四边形ABCD为平行四边形，面PAD⊥平面ABCD，PA=PD，Q为AD的中点，且QB⊥AD．（Ⅰ）求证：PB⊥BC；
（Ⅱ）若点M在PC上，且
| PM |
| MC |
| 1 |
| 2 |
考点：棱柱、棱锥、棱台的体积
专题：证明题
分析：（Ⅰ）由PA=PD，Q为AD的中点，得PQ⊥AD，又QB⊥AD，得到AD⊥平面QPB，再由BC∥AD，可得BC⊥面PQB，从而证明BC⊥PB．
（Ⅱ）不难得出PQ⊥面PBQ，设M到面ABCD的距离为h，则有
=
，得到
=
=
，再代入计算即可．
（Ⅱ）不难得出PQ⊥面PBQ，设M到面ABCD的距离为h，则有
| h |
| PQ |
| 2 |
| 3 |
| VC-MQB |
| VP-ABCD |
| VM-QBC |
| VP-ABCD |
| ||
|
解答：
（Ⅰ）证明：∵PA=PD，Q为AD的中点，
∴PQ⊥AD，PQ∩QB=Q，
∴AD⊥平面QPB，
∵四边形ABCD是平行四边形，∴BC∥AD，
∴BC⊥面PQB，
∴BC⊥PB．
（Ⅱ）由于面PAD⊥面ABCD，且PQ⊥AD，
∴PQ⊥面PBQ，
∴PQ的长即为四棱锥P-ABCD的高，
设M到面ABCD的距离为h，
则由
=
知，
=
，
∴h=
PQ．
设四边形ABCD的面积为S，
∴VC-MQB=VM-QBC=
×
Sh=
S•PQ，
∴
=
=
．
∴PQ⊥AD，PQ∩QB=Q，
∴AD⊥平面QPB，
∵四边形ABCD是平行四边形，∴BC∥AD，
∴BC⊥面PQB，
∴BC⊥PB．
（Ⅱ）由于面PAD⊥面ABCD，且PQ⊥AD，
∴PQ⊥面PBQ，
∴PQ的长即为四棱锥P-ABCD的高，
设M到面ABCD的距离为h，
则由
| PM |
| MC |
| 1 |
| 2 |
| h |
| PQ |
| 2 |
| 3 |
∴h=
| 2 |
| 3 |
设四边形ABCD的面积为S，
∴VC-MQB=VM-QBC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 9 |
∴
| VC-MQB |
| VP-ABCD |
| ||
|
| 1 |
| 3 |
点评：本题是对立体几何的综合考查，涉及到点、线、面的位置关系和立体几何中的计算问题，特别是计算体积时，“转化”是我们常见的方法，常见的有等体积法，割补法等等．
练习册系列答案
相关题目
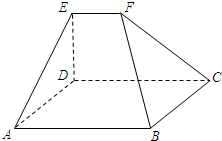如图，在五面体ABCDEF中，四边形ABCD是矩形，DE⊥平面ABCD．