题目内容
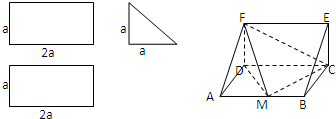 一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.
一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.(1)求证:CM⊥平面FDM;
(2)求直线DM与平面ABEF所成角的大小.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)先根据三视图可得直观图为直三棱柱,欲证CM⊥平面FDM,根据直线与平面垂直的判定定理可知只需证CM与平面FDM内两相交直线垂直,根据线面垂直的性质可知FD⊥CM,以及根据勾股定理可知CM⊥DM,FD?平面FDM,DM?平面FDM,满足定理所需条件;
(2)在平面ADF上,过D作AF的垂线,垂足为H,连DM,根据线面所成角的定义可知∠DMH是DM与平面ABEF所成的角,然后在三角形DHM中求出此角即可.
(2)在平面ADF上,过D作AF的垂线,垂足为H,连DM,根据线面所成角的定义可知∠DMH是DM与平面ABEF所成的角,然后在三角形DHM中求出此角即可.
解答:
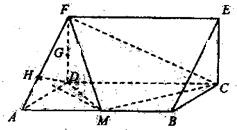 解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=a,
解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=a,
(1)显然FD⊥平面ABCD,
又CM?平面ABCD,
∴FD⊥CM(2分)
在矩形ABCD中,CD=2a,AD=a,
M为AB中点,DM=CM=
a,
∴CM⊥DM
∵FD?平面FDM,DM?平面FDM,
∴CM⊥平面FDM;
(2)在平面ADF上,过D作AF的垂线.
垂足为H,连DM,
则DH⊥平面ABEF,
∠DMH是DM与平面ABEF所成的角(12分)
在Rt△DHM中,DH=
a,DM=
a
∴sin∠DMH=
=
∴∠DMH=
.所以直线DM与平面ABEF所成角为
.
 解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=a,
解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=a,(1)显然FD⊥平面ABCD,
又CM?平面ABCD,
∴FD⊥CM(2分)
在矩形ABCD中,CD=2a,AD=a,
M为AB中点,DM=CM=
| 2 |
∴CM⊥DM
∵FD?平面FDM,DM?平面FDM,
∴CM⊥平面FDM;
(2)在平面ADF上,过D作AF的垂线.
垂足为H,连DM,
则DH⊥平面ABEF,
∠DMH是DM与平面ABEF所成的角(12分)
在Rt△DHM中,DH=
| ||
| 2 |
| 2 |
∴sin∠DMH=
| DH |
| DM |
| 1 |
| 2 |
∴∠DMH=
| π |
| 6 |
| π |
| 6 |
点评:本题主要考查直线与平面垂直的判定和直线与平面所成角的计算,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)是定义于R上的奇函数,当x≥0时,f(x)=|x-a|-a(a>0),且对任意x∈R,恒有f(x+1)≥f(x),则实数a的取值范围是( )
| A、(0,4] | ||
| B、(0,2] | ||
C、(0,
| ||
D、(0,
|
 设数列{an}是集合{3x+3s|0≤s<t,s,t∈Z}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大、左小右大的原则排场如图所示的等腰直角三角形数表,则a1000=
设数列{an}是集合{3x+3s|0≤s<t,s,t∈Z}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大、左小右大的原则排场如图所示的等腰直角三角形数表,则a1000=