题目内容
已知α,β是两个不同的平面,m,n是两条不同的直线,则下列命题正确的是( )
| A、α⊥β,m?α,则m⊥β |
| B、m∥n,n?α,则m∥α |
| C、m⊥α,m?β,则α⊥β |
| D、m∥α,n?a,则m∥n |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据面面垂直的几何特征及性质可判断A;根据线面平行的判定定理,可判断B;根据面面垂直的判定定理,可判断C;根据线面平行的几何特征,及空间线线关系的定义,可判断D.
解答:
解:若α⊥β,m?α,则m与β可能平行,可能相交,也可能线在面内,故A错误;
若m∥n,n?α,则m∥α或m?α,故B错误;
若m⊥α,m?β,则α⊥β,故C正确;
若m∥α,n?a,则m与n可能平行也可能异面,故D错误;
故选:C
若m∥n,n?α,则m∥α或m?α,故B错误;
若m⊥α,m?β,则α⊥β,故C正确;
若m∥α,n?a,则m与n可能平行也可能异面,故D错误;
故选:C
点评:本题考查的知识点是空间直线与平面之间的位置关系,熟练掌握空间线面关系,面面关系,线线关系的定义,几何特征及性质和判定方法是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式x(x-3)<0的解集是( )
| A、{x|x<0} |
| B、{x|x<3} |
| C、{x|0<x<3} |
| D、{x|x<0或x>3} |
研究发现,某公司年初三个月的月产值y(万元)与月份n近似地满足函数关系式y=an2+bn+c(如n=1表示1月份).已知1月份的产值为4万元,2月份的产值为11万元,3月份的产值为22万元.由此可预测4月份的产值为( )
| A、35万元 | B、37万元 |
| C、56万元 | D、79万元 |
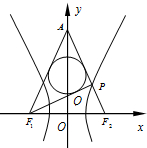 如图,已知双曲线
如图,已知双曲线