题目内容
不等式x(x-3)<0的解集是( )
| A、{x|x<0} |
| B、{x|x<3} |
| C、{x|0<x<3} |
| D、{x|x<0或x>3} |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:结合函数y=x(x-3)的图象,求得不等式x(x-3)<0的解集.
解答:
解:由不等式x(x-3)<0,结合函数y=x(x-3)的图象,
可得不等式x(x-3)<0的解集为 {x|0<x<3},
故选:C.
可得不等式x(x-3)<0的解集为 {x|0<x<3},
故选:C.
点评:本题主要考查一元二次不等式的解法,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设集合U={x∈N*|x≤4},A={1,2},B={2,4},则(∁UA)∪B=( )
| A、{1,2} |
| B、{1,2,3,4} |
| C、{3,4} |
| D、{2,3,4} |
已知三条直线a,b,c和平面β,则下列推论中正确的是( )
| A、若a∥b,b?β,则a∥β |
| B、若a∥β,b∥β,则a∥b或a与b相交 |
| C、若a⊥c,b⊥c,则a∥b |
| D、若a?β,b∥β,a,b共面,则a∥b |
若按如图的算法流程图运行后,输出的结果是
,则输入的N的值为( )

| 6 |
| 7 |

| A、5 | B、6 | C、7 | D、8 |
已知α,β是两个不同的平面,m,n是两条不同的直线,则下列命题正确的是( )
| A、α⊥β,m?α,则m⊥β |
| B、m∥n,n?α,则m∥α |
| C、m⊥α,m?β,则α⊥β |
| D、m∥α,n?a,则m∥n |
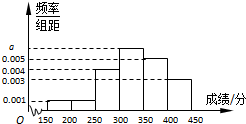 某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有
某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.