题目内容
在平面直角坐标系xoy中,已知曲线C1上的任一点到点(1,0)的距离与到直线x=2的距离之比为
,动点Q是动圆C2:x2+y2=r2(1<r<
)上一点.
(1)求曲线C1的轨迹方程;
(2)若点P为曲线C1上的点,直线PQ与曲线C1和动圆C2均只有一个公共点,求P、Q两点的距离|PQ|的最大值.
| ||
| 2 |
| 2 |
(1)求曲线C1的轨迹方程;
(2)若点P为曲线C1上的点,直线PQ与曲线C1和动圆C2均只有一个公共点,求P、Q两点的距离|PQ|的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据曲线C1上的任一点到点(1,0)的距离与到直线x=2的距离之比为
,建立方程,化简,即可求曲线C1的轨迹方程;
(2)易知直线PQ的斜率存在,设直线方程为y=kx+m,设P(x1,y1),Q(x2,y2),由
得(2k2+1)x12+4kmx1+2(m2-1)=0,由直线与椭圆相切得△=0,x1=-
①,由直线PQ与圆C2相切,则
=r②,联立①②可消掉m,由勾股定理可把|PQ|2表示为r的函数,再用基本不等式可得其最大值.
| ||
| 2 |
(2)易知直线PQ的斜率存在,设直线方程为y=kx+m,设P(x1,y1),Q(x2,y2),由
|
| 2k |
| m |
| |m| | ||
|
解答:
解:(1)设曲线C1上的任一点(x,y),依题意
∵曲线C1上的任一点到点(1,0)的距离与到直线x=2的距离之比为
,
∴
=
,化简方程得
+y2=1.…(3分)
(2)依题意可知直线PQ显然有斜率,设其方程为y=kx+m,
设P(x1,y1),Q(x2,y2),…(4分)
由于直线PQ与曲线C1相切,点P为切点,从而有
得(2k2+1)x12+4kmx1+2(m2-1)=0…(10分).
由于直线PQ与椭圆C1相切,故△=(4km)2-4×2(m2-1)(2k2+1)=0
从而可得m2=1+2k2,①x1=-
…(8分)
又直线PQ与圆C2相切,则
=r,
∴m2=r2(1+k2),②…(9分)
由①②得k2=
,…(10分)
并且|PQ|2=|OP|2-|OQ|2=x12+y12-r2=3-r2-
≤3-2
即|PQ|≤
-1,当且仅当r2=
∈(1,2)时取等号,…(13分)
故P、Q两点的距离|PQ|的最大值
-1.…(14分)
∵曲线C1上的任一点到点(1,0)的距离与到直线x=2的距离之比为
| ||
| 2 |
∴
| ||
| |x-2| |
| ||
| 2 |
| x2 |
| 2 |
(2)依题意可知直线PQ显然有斜率,设其方程为y=kx+m,
设P(x1,y1),Q(x2,y2),…(4分)
由于直线PQ与曲线C1相切,点P为切点,从而有
|
得(2k2+1)x12+4kmx1+2(m2-1)=0…(10分).
由于直线PQ与椭圆C1相切,故△=(4km)2-4×2(m2-1)(2k2+1)=0
从而可得m2=1+2k2,①x1=-
| 2k |
| m |
又直线PQ与圆C2相切,则
| |m| | ||
|
∴m2=r2(1+k2),②…(9分)
由①②得k2=
| r2-1 |
| 2-r2 |
并且|PQ|2=|OP|2-|OQ|2=x12+y12-r2=3-r2-
| 2 |
| r2 |
| 2 |
即|PQ|≤
| 2 |
| 2 |
故P、Q两点的距离|PQ|的最大值
| 2 |
点评:本题考查直线方程、椭圆方程及其位置关系,考查学生综合运用所学知识分析解决问题的能力,本题综合性强,难度大.

练习册系列答案
相关题目
已知三条直线a,b,c和平面β,则下列推论中正确的是( )
| A、若a∥b,b?β,则a∥β |
| B、若a∥β,b∥β,则a∥b或a与b相交 |
| C、若a⊥c,b⊥c,则a∥b |
| D、若a?β,b∥β,a,b共面,则a∥b |
按如图程序框图来计算,若输入x=10,则运算的次数为( )

| A、6 | B、5 | C、4 | D、3 |
已知α,β是两个不同的平面,m,n是两条不同的直线,则下列命题正确的是( )
| A、α⊥β,m?α,则m⊥β |
| B、m∥n,n?α,则m∥α |
| C、m⊥α,m?β,则α⊥β |
| D、m∥α,n?a,则m∥n |

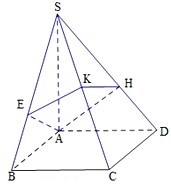 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.