题目内容
若函数f(x)=
-ln(x+1)不存在零点,则实数k的取值范围是 .
| lnkx |
| 2 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由题意可知
可得x>-1且x≠0,k=x+
+2,(x>-1且x≠0),由“对号函数”的性质和集合的运算可得.
|
| 1 |
| x |
解答:
解:由题意可知
,解得x>-1且x≠0,
由对数的性质可得lnkx=2ln(x+1)=ln(x+1)2,
可得kx=(x+1)2,变形可得k=
=x+
+2,(x>-1且x≠0)
由“对号函数”的性质可知x+
<-2,或x+
≥2,
∴x+
+2<0,或x+
+2≥4,
要使函数f(x)=
-ln(x+1)不存在零点,
只需k取x+
+2取值集合的补集,即{k|0≤k<4},
当k=0时,函数无意义,
故k的取值范围应为:(0,4)
故答案为:(0,4)
|
由对数的性质可得lnkx=2ln(x+1)=ln(x+1)2,
可得kx=(x+1)2,变形可得k=
| (x+1)2 |
| x |
| 1 |
| x |
由“对号函数”的性质可知x+
| 1 |
| x |
| 1 |
| x |
∴x+
| 1 |
| x |
| 1 |
| x |
要使函数f(x)=
| lnkx |
| 2 |
只需k取x+
| 1 |
| x |
当k=0时,函数无意义,
故k的取值范围应为:(0,4)
故答案为:(0,4)
点评:本题考查函数的零点,涉及“对号函数”的性质和集合的运算,属基础题.

练习册系列答案
相关题目
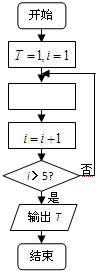 如图所示的程序框图,若执行的运算是1×
如图所示的程序框图,若执行的运算是1×| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•i | ||
| B、T=T•(i+1) | ||
C、T=T•
| ||
D、T=T•
|
已知α,β是两个不同的平面,m,n是两条不同的直线,则下列命题正确的是( )
| A、α⊥β,m?α,则m⊥β |
| B、m∥n,n?α,则m∥α |
| C、m⊥α,m?β,则α⊥β |
| D、m∥α,n?a,则m∥n |

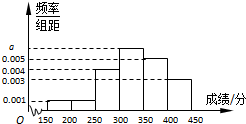 某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有
某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有