Question

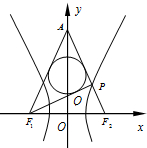如图，已知双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左右焦点分别为F₁，F₂，|F₁F₂|=4，P是双曲线右支上的一点，F₂P与y轴交于点A，△APF₁的内切圆在边PF₁上的切点为Q，若|PQ|=1，则双曲线的离心率是（　　）

• A、3
• B、2
• C、

  3

• D、

  2

Answer 1

考点：双曲线的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：由|PQ|=1，△APF₁的内切圆在边PF₁上的切点为Q，根据切线长定理，可得|PF₁|-|PF₂|=2，结合|F₁F₂|=4，即可得出结论．

解答： 解：由题意，∵|PQ|=1，△APF₁的内切圆在边PF₁上的切点为Q，
∴根据切线长定理，可得|PF₁|-|PF₂|=2，
∵|F₁F₂|=4，
∴双曲线的离心率是e=

c

a

=2．
故选：B．

点评：本题考查双曲线的离心率，考查三角形内切圆的性质，考查切线长定理，考查学生的计算能力，属于基础题．