题目内容
研究发现，某公司年初三个月的月产值y（万元）与月份n近似地满足函数关系式y=an2+bn+c（如n=1表示1月份）．已知1月份的产值为4万元，2月份的产值为11万元，3月份的产值为22万元．由此可预测4月份的产值为（ ）
| A、35万元 | B、37万元 |
| C、56万元 | D、79万元 |
考点：二次函数的性质
专题：函数的性质及应用
分析：利用已知条件列出方程组，求出a、b、c，得到函数的解析式，然后求解4月份的产值．
解答：
解：某公司年初三个月的月产值y（万元）与月份n近似地满足函数关系式y=an2+bn+c（如n=1表示1月份）．已知1月份的产值为4万元，2月份的产值为11万元，3月份的产值为22万元．
由此可得：
，
解得
，∴y=2n2+n+1，
∴可预测4月份的产值为：2×42+4+1=37．（万元）．
故选：B．
由此可得：
|
解得
|
∴可预测4月份的产值为：2×42+4+1=37．（万元）．
故选：B．
点评：本题考查函数的解析式的求法，函数的基本知识以及方程组的求法，考查计算能力．
练习册系列答案
相关题目
已知三条直线a，b，c和平面β，则下列推论中正确的是（ ）
| A、若a∥b，b?β，则a∥β |
| B、若a∥β，b∥β，则a∥b或a与b相交 |
| C、若a⊥c，b⊥c，则a∥b |
| D、若a?β，b∥β，a，b共面，则a∥b |
若按如图的算法流程图运行后，输出的结果是
，则输入的N的值为（ ）
| 6 |
| 7 |
| A、5 | B、6 | C、7 | D、8 |
按如图程序框图来计算，若输入x=10，则运算的次数为（ ）
| A、6 | B、5 | C、4 | D、3 |
已知α，β是两个不同的平面，m，n是两条不同的直线，则下列命题正确的是（ ）
| A、α⊥β，m?α，则m⊥β |
| B、m∥n，n?α，则m∥α |
| C、m⊥α，m?β，则α⊥β |
| D、m∥α，n?a，则m∥n |
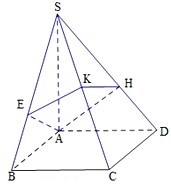如图，四棱锥S-ABCD的底面是正方形，侧棱SA⊥底面ABCD，过A作AE垂直SB交SB于E点，作AH垂直SD交SD于H点，平面AEH交SC于K点，P是SA上的动点，且AB=1，SA=2．