题目内容
已知正项数列{an},其前n项和Sn满足8Sn=an2+4an+3,且a2是a1和a7的等比中项.
(Ⅰ)求数列{
}的通项公式;
(Ⅱ)设bn=log2
,求数列{
}的前99项和.
(Ⅰ)求数列{
| a | n |
(Ⅱ)设bn=log2
| an+3 |
| 4(n+1) |
| b | n |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)在数列递推式8Sn=an2+4an+3中取n=n-1,得到8Sn-1=an-12+4an-1+3 (n≥2,n∈N),列式作差后可得{an}为公差为4的等差数列,再由已知递推式求得首项,则数列{
}的通项公式可求;
(Ⅱ)把数列{
}的通项公式代入bn=log2
,把数列{
}的前99项作和后由对数的运算性质化简求值.
| a | n |
(Ⅱ)把数列{
| a | n |
| an+3 |
| 4(n+1) |
| b | n |
解答:
解:(Ⅰ) 由8Sn=an2+4an+3 ①
得8Sn-1=an-12+4an-1+3 (n≥2,n∈N) ②
由①-②得8an=(an-an-1)(an+an-1)+4an-4an-1,
整理得(an-an-1-4)(an+an-1)=0(n≥2,n∈N),
∵{an}为正项数列
∴an+an-1>0,
∴an-an-1=4(n≥2,n∈N),
∴{an}为公差为4的等差数列,
由8a1=a12+4a1+3,得a1=3或a1=1.
当a1=3时,a2=7,a7=27,不满足a2是a1和a7的等比中项.
当a1=1时,a2=5,a7=25,满足a2是a1和a7的等比中项.
∴an=1+(n-1)4=4n-3.
(Ⅱ)由an=4n-3,得bn=log2(
)=log2
,
∴b1+b2+b3+…b99=log2
+log2
+log2
+…log2
=log2
×
×
…×
=log2
=-log2100=-2-2log25.
得8Sn-1=an-12+4an-1+3 (n≥2,n∈N) ②
由①-②得8an=(an-an-1)(an+an-1)+4an-4an-1,
整理得(an-an-1-4)(an+an-1)=0(n≥2,n∈N),
∵{an}为正项数列
∴an+an-1>0,
∴an-an-1=4(n≥2,n∈N),
∴{an}为公差为4的等差数列,
由8a1=a12+4a1+3,得a1=3或a1=1.
当a1=3时,a2=7,a7=27,不满足a2是a1和a7的等比中项.
当a1=1时,a2=5,a7=25,满足a2是a1和a7的等比中项.
∴an=1+(n-1)4=4n-3.
(Ⅱ)由an=4n-3,得bn=log2(
| an+3 |
| 4(n+1) |
| n |
| n+1 |
∴b1+b2+b3+…b99=log2
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 99 |
| 100 |
=log2
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 99 |
| 100 |
| 1 |
| 100 |
点评:本题考查了数列递推式,考查了等差关系的确定,训练了对数的运算性质,是中档题.

练习册系列答案
相关题目
若按如图的算法流程图运行后,输出的结果是
,则输入的N的值为( )

| 6 |
| 7 |

| A、5 | B、6 | C、7 | D、8 |
已知α,β是两个不同的平面,m,n是两条不同的直线,则下列命题正确的是( )
| A、α⊥β,m?α,则m⊥β |
| B、m∥n,n?α,则m∥α |
| C、m⊥α,m?β,则α⊥β |
| D、m∥α,n?a,则m∥n |
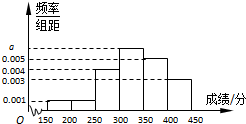 某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有
某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有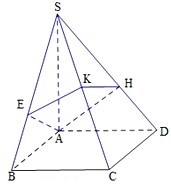 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2. 如图示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于C,若|BC|=2|BF|,且|AC|=5,求此抛物线的方程.
如图示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于C,若|BC|=2|BF|,且|AC|=5,求此抛物线的方程. 已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.