题目内容
已知椭圆的两个焦点为F1、F2,|F1F2|=14,P为椭圆上一点,∠F1PF2=
π,若△F1PF2的面积S=13
,求椭圆的标准方程.
| 2 |
| 3 |
| 3 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设椭圆的标准方程为
+
=1,(a>b>0),|PF1|=m,|PF2|=n,由已知知mn=52,m2+n2-2mncos120°=142,由此求出椭圆方程为
+
=1.同理,设椭圆方程为
+
=1,(a>b>0),解得椭圆方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 62 |
| y2 |
| 13 |
| x2 |
| b2 |
| y2 |
| a2 |
| x2 |
| 13 |
| y2 |
| 62 |
解答:
解:设椭圆的标准方程为
+
=1,(a>b>0),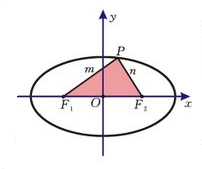
|PF1|=m,|PF2|=n,
∵S△PF1F2=13
,∴
mnsin120°=13
,
解得mn=52,①
△PF1F2中,|F1F2|=14,
∴m2+n2-2mncos120°=142,②
由①②,得(m+n)2=m2+n2+2mn=142+52=248,
∴4a2=248,解得a2=62,
又c2=49,∴b2=a2-c2=13,
∴椭圆方程为
+
=1.
同理,设椭圆方程为
+
=1,(a>b>0),
解得椭圆方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |

|PF1|=m,|PF2|=n,
∵S△PF1F2=13
| 3 |
| 1 |
| 2 |
| 3 |
解得mn=52,①
△PF1F2中,|F1F2|=14,
∴m2+n2-2mncos120°=142,②
由①②,得(m+n)2=m2+n2+2mn=142+52=248,
∴4a2=248,解得a2=62,
又c2=49,∴b2=a2-c2=13,
∴椭圆方程为
| x2 |
| 62 |
| y2 |
| 13 |
同理,设椭圆方程为
| x2 |
| b2 |
| y2 |
| a2 |
解得椭圆方程为
| x2 |
| 13 |
| y2 |
| 62 |
点评:本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
相关题目
已知定义在R上的函数f(x)满足f(x)•f(x+
π)=-1.若f(
)=2,则f(11π)等于( )
| 3 |
| 2 |
| π |
| 2 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |