题目内容
设复数=x+yi(x,y∈R,i为虚数单位).
(1)若(x2-3)+yi=1+2i,且复数在复平面内对应的点在第二象限,求复数z;
(2)若y=1,且
是实数,求|z|.
(1)若(x2-3)+yi=1+2i,且复数在复平面内对应的点在第二象限,求复数z;
(2)若y=1,且
| z |
| 1-i |
考点:复数求模,复数代数形式的混合运算
专题:数系的扩充和复数
分析:(1)由复数相等的条件列式求解x,y的值,结合复数在复平面内对应的点在第二象限进一步求得z;
(2)把z代入
,由复数代数形式的乘除运算化简后由虚部等于0求得x的值,再由复数模的公式求模.
(2)把z代入
| z |
| 1-i |
解答:
解:(1)由(x2-3)+yi=1+2i,得
,解得
或
.
∵复数z=x+yi在复平面内对应的点在第二象限,
∴
.
故z=-2+2i;
(2)由y=1,且
=
=
=
是实数,得x=-1.
∴z=-1+i,
∴|z|=
=
.
|
|
|
∵复数z=x+yi在复平面内对应的点在第二象限,
∴
|
故z=-2+2i;
(2)由y=1,且
| z |
| 1-i |
| x+i |
| 1-i |
| (x+i)(1+i) |
| (1-i)(1+i) |
| x-1+(x+1)i |
| 2 |
∴z=-1+i,
∴|z|=
| (-1)2+12 |
| 2 |
点评:本题考查了复数代数形式的乘除运算,考查了复数相等的条件,训练了复数模的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在同一坐标系中,将曲线y=2sin3x变为曲线y=sinx的伸缩变换公式是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
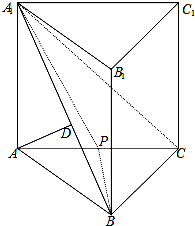 如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.