题目内容
已知函数f(x)=x|x-a|+b.
(1)若函数f(x)是奇函数,求f(x)的表达式;
(2)若a>0,b=-2,当x∈[0,1]时,恒有f(x)不大于零,求实数a的取值范围.
(1)若函数f(x)是奇函数,求f(x)的表达式;
(2)若a>0,b=-2,当x∈[0,1]时,恒有f(x)不大于零,求实数a的取值范围.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据函数是奇函数,f(0)=0,f(-x)=-f(x)求解f(x)的表达式;
(2)分情况讨论去掉绝对值,然后利用函数的单调性求a的取值范围.
(2)分情况讨论去掉绝对值,然后利用函数的单调性求a的取值范围.
解答:
 解:因为f(x)=x|x-a|+b,
解:因为f(x)=x|x-a|+b,
所以f(-x)=(-x)|(-x)-a|+b=-x|x+a|+b,
又f(x)是奇函数,
所以f(-x)=-f(x),
即-x|x+a|+b=-x|x-a|-b,
即x(|x-a|-|x+a|)-2b=0,
又f(0)=0⇒b=0,
所以x(|x-a|-|x+a|)=0,
所以|x-a|=|x+a|,
两边平分得:(x-a)2=(x+a)2,即x2-2ax+a2=x2+2ax+a2,
所以2ax=0
解得:a=0
故f(x)=x|x|;
(2)b=-2时,f(x)=
图象如图:
①当
>1,即a>2时,只需f(1)≤0,-1+a-2≤0,解得2<a≤3;
②当
≤1<a,即1<a≤2时,只需f(x)max=f(
)≤0,即
-2≤0,解得:1<a≤2;
③当a≤1时,函数在[0,1]上先减后增,
⇒
,解得-1≤a≤1,
综上:-1≤a≤3.
 解:因为f(x)=x|x-a|+b,
解:因为f(x)=x|x-a|+b,所以f(-x)=(-x)|(-x)-a|+b=-x|x+a|+b,
又f(x)是奇函数,
所以f(-x)=-f(x),
即-x|x+a|+b=-x|x-a|-b,
即x(|x-a|-|x+a|)-2b=0,
又f(0)=0⇒b=0,
所以x(|x-a|-|x+a|)=0,
所以|x-a|=|x+a|,
两边平分得:(x-a)2=(x+a)2,即x2-2ax+a2=x2+2ax+a2,
所以2ax=0
解得:a=0
故f(x)=x|x|;
(2)b=-2时,f(x)=
|
①当
| a |
| 2 |
②当
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
③当a≤1时,函数在[0,1]上先减后增,
|
|
综上:-1≤a≤3.
点评:本题主要考查奇函数的性质和函数的单调性,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
设甲、乙两名射手各打了5发子弹,每发子弹击中环数如下:
甲:10,6,7,10,8;
乙:8,7,9,10,9
则甲、乙两名射手的射击技术评定情况是( )
甲:10,6,7,10,8;
乙:8,7,9,10,9
则甲、乙两名射手的射击技术评定情况是( )
| A、甲比乙好 | B、乙比甲好 |
| C、甲、乙一样好 | D、难以确定 |
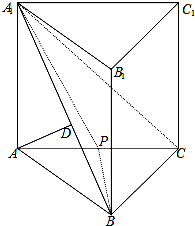 如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.