题目内容
16.设F1、F2分别是椭圆的左、右焦点,坐标分别是(-2,0)、(2,0),椭圆离心率为60°角的正弦值(1)求椭圆的标准方程;
(2)若P是该椭圆上的一个动点,求$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最大值和最小值;
(3)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
分析 (1)根据椭圆焦点及离心率求得焦点在x轴的椭圆标准方程.
(2)运用数量积的坐标运算,及函数思想,求得最值.
(3)运用设而不求法及数量积为负,求得直线l的斜率取值范围.
解答 解:(1)由题知椭圆焦点在x轴,故设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0).
椭圆离心率为60°角的正弦值,
∴$e=\frac{\sqrt{3}}{2}$=$\frac{c}{a}$
又c=2,且b2=a2-c2,
∴a2=$\frac{16}{3}$,${b}^{2}=\frac{4}{3}$
∴椭圆标准方程为:$\frac{{x}^{2}}{\frac{16}{3}}+\frac{{y}^{2}}{\frac{4}{3}}=1$
(2)设椭圆上动点P(m,n),则${n}^{2}=\frac{4}{3}-\frac{{m}^{2}}{4}$
$\overrightarrow{P{F}_{1}}=(-2-m,-n)$,$\overrightarrow{P{F}_{2}}=(2-m,-n)$
则$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=(-2-m)(2-m)+n2=$\frac{3}{4}{m}^{2}-\frac{8}{3}$
∵${m}^{2}∈[0,\frac{16}{3}]$
∴$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}∈$$[-\frac{8}{3},\frac{4}{3}]$
则$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$的最大值为$\frac{4}{3}$,最小值为$-\frac{8}{3}$.
(3)由题知斜率不存在时,不符合题意.
故设A(x1,y1),B(x2,y2),直线l的方程为y=kx+2,
$\left\{\begin{array}{l}{\frac{{x}^{2}}{\frac{16}{3}}+\frac{{y}^{2}}{\frac{4}{3}}=1}\\{y=kx+2}\end{array}\right.$,得(3+12k2)x2+48kx+32=0
△>0,得${k}^{2}>\frac{1}{2}$.
${x}_{1}+{x}_{2}=\frac{-48k}{3+12{k}^{2}}$,${x}_{1}{x}_{2}=\frac{32}{3+12{k}^{2}}$
∠AOB为锐角,则$\overrightarrow{OA}•\overrightarrow{OB}>0$
又$\overrightarrow{OA}•\overrightarrow{OB}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}$
=(1+k2)x1x2+2k(x1+x2)+4
=$\frac{32(1+{k}^{2})}{3+12{k}^{2}}$$-\frac{96{k}^{2}}{3+12{k}^{2}}$+4
∴$\frac{32(1+{k}^{2})}{3+12{k}^{2}}$$-\frac{96{k}^{2}}{3+12{k}^{2}}$+4>0
化简得:11-4k2>0 即${k}^{2}<\frac{11}{4}$
∴$\frac{1}{2}<{k}^{2}<\frac{11}{4}$
故直线l的斜率k的取值范围为$-\frac{\sqrt{11}}{2}<k<-\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{2}<k<\frac{\sqrt{11}}{2}$.
点评 考查椭圆标准方程求解,椭圆中的函数思想,椭圆中的设而不求法.考查划归思想处理角为锐角.难度不大,属于中档题.

 寒假学与练系列答案
寒假学与练系列答案| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
| A. | (-2,1) | B. | [-2,1) | C. | [-1,2) | D. | (-1,2) |
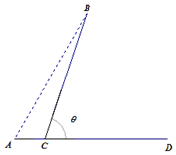 某城市A计划每天从蔬菜基地B处给本市供应蔬菜,为此,准备从主干道AD的C处(不在端点A、D处)做一条道路CB,主干道AD的长为60千米,设计路线如图所示,测得蔬菜基地B在城市A的东偏北60°处,AB长为60千米,设∠BCD=θ,运输汽车在主干道AD上的平均车速为60千米/小时,在道路CB上的平均车速为20千米/小时.
某城市A计划每天从蔬菜基地B处给本市供应蔬菜,为此,准备从主干道AD的C处(不在端点A、D处)做一条道路CB,主干道AD的长为60千米,设计路线如图所示,测得蔬菜基地B在城市A的东偏北60°处,AB长为60千米,设∠BCD=θ,运输汽车在主干道AD上的平均车速为60千米/小时,在道路CB上的平均车速为20千米/小时.