题目内容
7．已知方程$\frac{{x}^{2}}{k-5}$+$\frac{{y}^{2}}{3+k}$=-1表示椭圆，求k的取值范围．（-∞，-3）．分析 化曲线方程为椭圆的标准方程，由分母大于0且不相等求得k的取值范围．
解答 解：由$\frac{{x}^{2}}{k-5}$+$\frac{{y}^{2}}{3+k}$=-1，得$\frac{{x}^{2}}{5-k}+\frac{{y}^{2}}{-3-k}=1$，
∵方程$\frac{{x}^{2}}{k-5}$+$\frac{{y}^{2}}{3+k}$=-1表示椭圆，
∴$\left\{\begin{array}{l}{5-k＞0}\\{-3-k＞0}\\{5-k≠-3-k}\end{array}\right.$，解得k＜-3．
∴k的取值范围是（-∞，-3）．
故答案为：（-∞，-3）．
点评 本题考查椭圆的标准方程，是基础的计算题．
练习册系列答案
相关题目
15．已知集合A={x|2x+2＜1}，B={x|x2-2x-3＞0}，则（∁RA）∩B=（ ）
| A． | [-2，-1） | B． | （-∞，-2] | C． | [-2，-1）∪（3，+∞） | D． | （-2，-1）∪（3，+∞） |
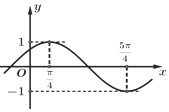已知函数$f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示．
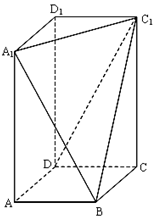已知长方体ABCD-A1B1C1D1，其中AB=BC=2，过A1、C1、B三点的平面截去长方体的一个角后．得到如图所示的，且这个几何体的体积为$\frac{40}{3}$．