题目内容
5.已知函数f(x)满足f(x+2)=f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有四个零点,则实数k的取值范围是(0,$\frac{1}{4}$].分析 根据题意知函数是一个偶函数且周期是2,画出函数的图象,数形结合,可得函数g(x)=f(x)-kx-k有四个零点,即函数f(x)的图象与y=kx+k的图象有四个交点时,实数k的取值范围.
解答 解:由于f(x+2)=f(x).
∴f(x)是周期为2的函数,
∵x∈[0,1]时,f(x)=x 由于f(x)是偶函数,
∴x∈[-1,0],f(x)=-x,
函数的图象如下图所示:
若函数g(x)=f(x)-kx-k有四个零点,
则函数f(x)的图象与y=kx+k的图象有四个交点,
由y=kx+k的图象必过(-1,0)点,且过(3,1)点时,k=$\frac{1}{4}$,
由图可得:k∈(0,$\frac{1}{4}$],
故答案为:(0,$\frac{1}{4}$]
点评 本题考查的知识点是根的存在性及根的个数判断,数形结合思想,难度中档.

练习册系列答案
相关题目
15.已知集合A={x|2x+2<1},B={x|x2-2x-3>0},则(∁RA)∩B=( )
| A. | [-2,-1) | B. | (-∞,-2] | C. | [-2,-1)∪(3,+∞) | D. | (-2,-1)∪(3,+∞) |
15.在区间$[{-\frac{π}{4},\frac{2π}{3}}]$上任取一个数x,则函数$f(x)=3sin({2x-\frac{π}{6}})$的值不小于0的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{11}$ | D. | $\frac{7}{12}$ |
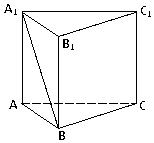 如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;
如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;