题目内容
1.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,已知点P(0,$\frac{3}{2}$)到椭圆上的点的最远距离是$\frac{7}{4}$,则短半轴之长b=( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 由$\frac{c}{a}=\frac{\sqrt{3}}{2}$,a2=b2+c2,可得:椭圆的标准方程为:x2+4y2=4b2.可设椭圆上的任意一点Q(x,y),则x2=4b2-4y2,(-b≤y≤b).|PQ|=$\sqrt{{x}^{2}+(y-\frac{3}{2})^{2}}$=$\sqrt{-3(y+\frac{1}{2})^{2}+4{b}^{2}+3}$.对b与$\frac{1}{2}$的大小关系分类讨论,利用二次函数的单调性即可得出.
解答 解:由$\frac{c}{a}=\frac{\sqrt{3}}{2}$,a2=b2+c2,可得:c2=3b2,a2=4b2.
∴椭圆的标准方程为:x2+4y2=4b2.
可设椭圆上的任意一点Q(x,y),则x2=4b2-4y2,(-b≤y≤b).
∴|PQ|=$\sqrt{{x}^{2}+(y-\frac{3}{2})^{2}}$=$\sqrt{-3(y+\frac{1}{2})^{2}+4{b}^{2}+3}$.
①若-b>-$\frac{1}{2}$即0<b$<\frac{1}{2}$,则当y=-b时|PQ|2最大,即$(-b-\frac{3}{2})^{2}$=$(\frac{7}{4})^{2}$,解得b=$\frac{1}{4}$.
②若-b≤-$\frac{1}{2}$≤b,即$b≥\frac{1}{2}$时,y=-$\frac{1}{2}$时,4b2+3=$(\frac{7}{4})^{2}$,解得b=$\frac{1}{8}$,与$b≥\frac{1}{2}$矛盾,舍去.
综上可得:b=$\frac{1}{4}$.
故选:C.
点评 本题考查了椭圆的标准方程及其性质、二次函数的单调性、两点之间的距离公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | (-∞,9] | B. | (-∞,18] | C. | [9,+∞) | D. | [18,+∞) |
| A. | (3,+∞) | B. | (3,4] | C. | (4,+∞) | D. | [4,+∞) |
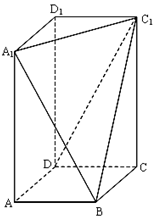 已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.
已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.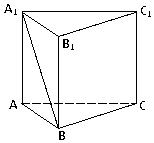 如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;
如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°; 已知函数f(x)=sin(2x+$\frac{π}{4}$)+1.
已知函数f(x)=sin(2x+$\frac{π}{4}$)+1.