题目内容
6.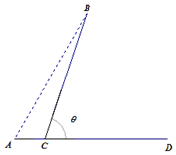 某城市A计划每天从蔬菜基地B处给本市供应蔬菜,为此,准备从主干道AD的C处(不在端点A、D处)做一条道路CB,主干道AD的长为60千米,设计路线如图所示,测得蔬菜基地B在城市A的东偏北60°处,AB长为60千米,设∠BCD=θ,运输汽车在主干道AD上的平均车速为60千米/小时,在道路CB上的平均车速为20千米/小时.
某城市A计划每天从蔬菜基地B处给本市供应蔬菜,为此,准备从主干道AD的C处(不在端点A、D处)做一条道路CB,主干道AD的长为60千米,设计路线如图所示,测得蔬菜基地B在城市A的东偏北60°处,AB长为60千米,设∠BCD=θ,运输汽车在主干道AD上的平均车速为60千米/小时,在道路CB上的平均车速为20千米/小时.(1)求运输汽车从城市A到蔬菜基地B处所用的时间t关于θ的函数关系式t(θ),并指出其定义域;
(2)求运输汽车从城市A到蔬菜基地B处所用的时间t的最小值.
分析 (1)求出BC,AC,可得运输汽车从城市A到蔬菜基地B处所用的时间t关于θ的函数关系式t(θ),并指出其定义域;
(2)求导数,确定函数的单调性,即可求运输汽车从城市A到蔬菜基地B处所用的时间t的最小值.
解答 解:(1)在△ABC中,$\frac{AB}{sin(π-θ)}=\frac{BC}{{sin\frac{π}{3}}}$,则$BC=\frac{{60•\frac{{\sqrt{3}}}{2}}}{sinθ}=\frac{{30\sqrt{3}}}{sinθ}$,…(2分)
又$\frac{AC}{{sin(θ-\frac{π}{3})}}=\frac{AB}{sin(π-θ)}$,则$AC=\frac{{60sin(θ-\frac{π}{3})}}{sinθ}$,…(4分)
所以,运输汽车从城市A到蔬菜基地B处所用的时间t(θ)=$\frac{AC}{60}+\frac{BC}{20}=\frac{{\frac{{60sin(θ-\frac{π}{3})}}{sinθ}}}{60}+\frac{{\frac{{30\sqrt{3}}}{sinθ}}}{20}$=$\frac{{sin(θ-\frac{π}{3})}}{sinθ}+\frac{{3\sqrt{3}}}{2sinθ}$=$\frac{{sinθ-\sqrt{3}cosθ+3\sqrt{3}}}{2sinθ}$=$\frac{1}{2}+\frac{{3\sqrt{3}-\sqrt{3}cosθ}}{2sinθ}$,
其定义域为{θ|60°<θ<120°}.…(6分)
(2)$t'(θ)=\frac{{\sqrt{3}}}{2}•\frac{(3-cosθ)'sinθ-(3-cosθ)(sinθ)'}{{{{sin}^2}θ}}$=$\frac{{\sqrt{3}}}{2}•\frac{1-3cosθ}{{{{sin}^2}θ}}$,…(9分)
令t'(θ)=0,则$cosθ=\frac{1}{3}$,
当$cosθ>\frac{1}{3}$时,t'(θ)>0;当$cosθ<\frac{1}{3}$时,t'(θ)<0,…(12分)
所以,当$cosθ=\frac{1}{3}$时,因为60°≤θ≤120°,所以$sinθ=\frac{{2\sqrt{2}}}{3}$时,t(θ)取得最小值,此时,最小值为$\frac{1}{2}+\sqrt{6}$.
答:运输汽车从城市A到蔬菜基地B处所用的时间t的最小值为$\frac{1}{2}+\sqrt{6}$.…(14分)
点评 本题考查导数知识的综合运用,考查正弦定理,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | (-∞,9] | B. | (-∞,18] | C. | [9,+∞) | D. | [18,+∞) |
| A. | [-2,-1) | B. | (-∞,-2] | C. | [-2,-1)∪(3,+∞) | D. | (-2,-1)∪(3,+∞) |