题目内容
8.“对称数”是指从左到右读与从右到左读都一样的正整数,如121,666,54345等,则在所有的六位数中,不同的“对称数”的个数是( )| A. | 100 | B. | 900 | C. | 999 | D. | 1000 |
分析 根据题意,对6位对称数,由于个位和十万位相同,十位和万位相同,百位和千位相同,个位有9种,十位和百位均有10种,由分步计数原理计算可得答案.
解答 解:根据题意,对6位对称数,由于个位和十万位相同,十位和万位相同,百位和千位相同,
个位有9种,十位和百位均有10种,故根据分步计数原理可得共有9×10×10=900
故选:B.
点评 本题考查排列、组合综合应用,关键是理解对称数的概念,属于基础题.

练习册系列答案
相关题目
18.若由曲线y=x2+k2与直线y=2kx及y轴所围成的平面图形的面积S=9,则k=( )
| A. | 3$\sqrt{3}$ | B. | -3或3 | C. | 3 | D. | -3 |
19.已知集合A={x|$\frac{3x-4}{2-x}$≥0},B={x|x2-2x<0},则A∩B=( )
| A. | [$\frac{4}{3}$,2) | B. | [$\frac{3}{4}$,2] | C. | ($\frac{3}{4}$,2) | D. | (-$∞,\frac{3}{4}$)∪(2,+∞) |
3.设复数z满足iz=1+2i,则复数z的共轭复数$\overline{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.设a∈R,若复数z=$\frac{a-i}{3+i}$(i是虚数单位)的实部为$\frac{1}{2}$,则a的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | -2 | D. | 2 |
18.锐角三角形ABC的三边长a,b,c成等差数列,且a2+b2+c2=21,则实数b的取值范围是( )
| A. | $({\sqrt{6},\sqrt{7}}]$ | B. | $({0,\sqrt{7}}]$ | C. | $({\frac{{2\sqrt{42}}}{5},\sqrt{7}}]$ | D. | (6,7] |
 如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上)
如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上) 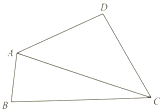 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.