题目内容
13.若m为正整数,则${∫}_{-1}^{1}$x(x+sin2mx)dx=$\frac{2}{3}$.分析 将被积函数变形,两条定积分的可加性以及微积分基本定理求值.
解答 解:m为正整数,则${∫}_{-1}^{1}$x(x+sin2mx)dx=${∫}_{-1}^{1}$(x2+xsin2mx)dx=2${∫}_{0}^{1}{x}^{2}dx$+${∫}_{-1}^{1}xsi{n}^{2}mxdx$=2×$\frac{1}{3}{x}^{3}{|}_{0}^{1}$+0=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$.
点评 本题考查定积分的计算;利用被积函数的原函数或者奇偶性求定积分.

练习册系列答案
相关题目
3.函数$f(x)={(\frac{1}{2})^x}$与g(x)=-|x|在区间(-∞,0)上的单调性为( )
| A. | 都是增函数 | B. | f(x)为减函数,g(x)为增函数 | ||
| C. | 都是减函数 | D. | f(x)为增函数,g(x)为减函数 |
1.某四棱锥的三视图如图所示,则该四棱锥的侧面积为( )
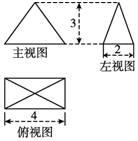

| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 2$\sqrt{10}$+$\sqrt{13}$ | D. | 4$\sqrt{10}$+2$\sqrt{13}$ |
8.“对称数”是指从左到右读与从右到左读都一样的正整数,如121,666,54345等,则在所有的六位数中,不同的“对称数”的个数是( )
| A. | 100 | B. | 900 | C. | 999 | D. | 1000 |
5.定义域为R的函数f(x)满足f(x+2)=$\sqrt{3}$f(x),x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{2{x}^{2}-2x,x∈[0,1)}\\{-2•(\frac{1}{3})^{|x-\frac{4}{3}|},x∈[1,2)}\end{array}\right.$,x
∈[-4,-2)时,f(x)≥t2-$\frac{7}{3}$t恒成立,则实数t的取值范围是( )
∈[-4,-2)时,f(x)≥t2-$\frac{7}{3}$t恒成立,则实数t的取值范围是( )
| A. | [$\frac{1}{2}$,3) | B. | (-∞,$\frac{1}{2}$]∪(3,+∞) | C. | [$\frac{1}{3}$,2] | D. | (-∞,$\frac{1}{3}$]∪[2,+∞) |
2.若$\frac{1+cosα}{sinα}$=2,则cosα-3sinα=( )
| A. | -3 | B. | 3 | C. | -$\frac{9}{5}$ | D. | $\frac{9}{5}$ |
3.某渔业公司为了解投资收益情况,调查了旗下的养鱼场和远洋捕捞队近10个月的利润情况.根据所收集的数据得知,近10个月总投资养鱼场一千万元,获得的月利润频数分布表如下:
近10个月总投资远洋捕捞队一千万元,获得的月利润频率分布直方图如下:
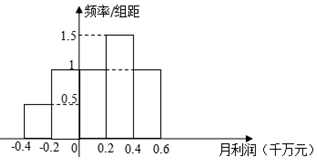
(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼
场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
| 月利润(单位:千万元) | -0.2 | -0.1 | 0 | 0.1 | 0.3 |
| 频数 | 2 | 1 | 2 | 4 | 1 |

(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼
场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.