题目内容
关于x的不等式x2-4ax+3a2<0(a>0)的解集为(x1,x2),则x1+x2+
的最小值是( )
| a |
| x1x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由不等式x2-4ax+3a2<0(a>0)的解集为(x1,x2),利用根与系数的关系可得x1+x2,x1x2,再利用基本不等式即可得出.
解答:
解:∵关于x的不等式x2-4ax+3a2<0(a>0)的解集为(x1,x2),
∴△=16a2-12a2=4a2>0,又a>0,可得a>0.
∴x1+x2=4a,x1x2=3a2,
∴x1+x2+
=4a+
=4a+
≥2
=
,当且仅当a=
时取等号.
∴x1+x2+
的最小值是
.
故选:C.
∴△=16a2-12a2=4a2>0,又a>0,可得a>0.
∴x1+x2=4a,x1x2=3a2,
∴x1+x2+
| a |
| x1x2 |
| a |
| 3a2 |
| 1 |
| 3a |
4a•
|
4
| ||
| 3 |
| ||
| 6 |
∴x1+x2+
| a |
| x1x2 |
4
| ||
| 3 |
故选:C.
点评:本题考查了一元二次不等式解集与相应的一元二次方程的实数根的关系、根与系数的关系、基本不等式的性质,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知点G是△ABC的重心,若∠A=120°,
•
=-2,则|
|的最小值是( )
| AB |
| AC |
| AG |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
“0<x<2”是“x2-x<0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
在(-π,2π)内与
终边相同的角有( )个.
| 3π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
设a=log54,b=(log53)2,c=log45,则a,b,c的大小关系为( )
| A、a<c<b |
| B、b<a<c |
| C、a<b<c |
| D、b<c<a |
已知方程组
对此方程组的每一组正实数解(x,y,z,u),其中z≥y,都存在正实数M,且满足M≤
,则M的最大值是( )
|
| z |
| y |
| A、1 | ||
B、3+2
| ||
C、6+4
| ||
D、3-2
|
利用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=4的值的时候需要做乘法和加法的次数分别为( )??
| A、6?6 | B、5?6 |
| C、5?5 | D、6?5 |
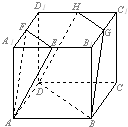 如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点,
如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点,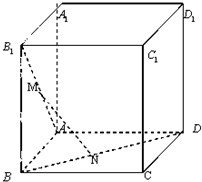 如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<
如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<