题目内容
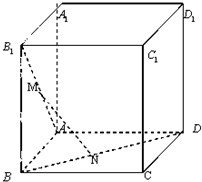 如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<
如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<| 2 |
(1)求|MN|的最小值
(2)当|MN|达到最小值时,
| MN |
| AB |
| BD |
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)作ME⊥AB于E,连EN.在△EBN中,由余弦定理可得EN,在△MEN中,由勾股定理可得MN,从而可求|MN|的最小值
(2)建立空间直角坐标系,求出
=(
,
,-
),
=(1,0,1),
=(-1,1,0),利用向量的数量积公式,即可得出结论.
(2)建立空间直角坐标系,求出
| MN |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| AB1 |
| BD |
解答:
 解:(1)作ME⊥AB于E,连EN.
解:(1)作ME⊥AB于E,连EN.
∵AM=BN=t,
∴ME=AE=
t,BE=1-
t,
∴在△EBN中,由余弦定理可得:EN2=t2+(1-
t)2-2t(1-
t)•
=
t2-2
t+1,
∴在△MEN中,由勾股定理可得MN2=3t2-2
t+1.
∴当t=
时,|
|最小值为
;
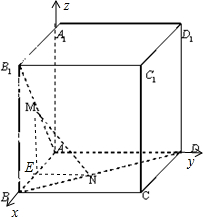
(2)建立如图所示的坐标系,由(1)知当|MN|达到最小值时,t=
,则
A(0,0,0),B1(1,0,1),B(1,0,0),D(0,1,0),M(
,0,
),N(
,
,0),
∴
=(
,
,-
),
=(1,0,1),
=(-1,1,0),
∴
•
=0,
•
=
,
∴
⊥
,
与
不垂直.
 解:(1)作ME⊥AB于E,连EN.
解:(1)作ME⊥AB于E,连EN.∵AM=BN=t,
∴ME=AE=
| ||
| 2 |
| ||
| 2 |
∴在△EBN中,由余弦定理可得:EN2=t2+(1-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| 2 |
∴在△MEN中,由勾股定理可得MN2=3t2-2
| 2 |
∴当t=
| ||
| 3 |
| MN |
| 1 |
| 3 |
(2)建立如图所示的坐标系,由(1)知当|MN|达到最小值时,t=
| ||
| 3 |
A(0,0,0),B1(1,0,1),B(1,0,0),D(0,1,0),M(
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴
| MN |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| AB1 |
| BD |
∴
| MN |
| AB1 |
| MN |
| BD |
| 1 |
| 3 |
∴
| MN |
| AB1 |
| MN |
| BD |
点评:本题考查空间距离的计算,考查向量知识的运用,正确表示向量是关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
关于x的不等式x2-4ax+3a2<0(a>0)的解集为(x1,x2),则x1+x2+
的最小值是( )
| a |
| x1x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
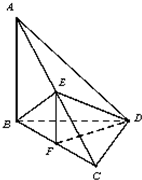 如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.
如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.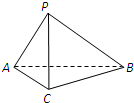 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.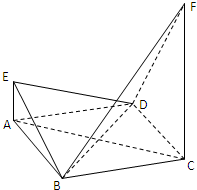 已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.
已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.