题目内容
“0＜x＜2”是“x2-x＜0”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质以及充分条件和必要条件的定义进行判断．
解答：
解：由x2-x＜0得0＜x＜1，
∴当0＜x＜2时，0＜x＜1不一定成立，
当0＜x＜1时，0＜x＜2一定成立，
∴“0＜x＜2”是“x2-x＜0”的必要不充分条件．
故选：B．
∴当0＜x＜2时，0＜x＜1不一定成立，
当0＜x＜1时，0＜x＜2一定成立，
∴“0＜x＜2”是“x2-x＜0”的必要不充分条件．
故选：B．
点评：本题主要考查充分条件和必要条件的判断，比较基础．
练习册系列答案
相关题目
设f（x）=x2-2x-4lnx，则f′（x）＜0的解集为（ ）
| A、（2，+∞） |
| B、（-1，0）U（2，+∞） |
| C、（-1，2） |
| D、（0，2） |
圆x2+y2+2y=1的半径为（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
函数y=1-
sinx的单调区间是（ ）
| 2 |
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
已知面α⊥β，α∩β=l，直线a?α，直线b?β，a，b与l斜交，则（ ）
| A、a和b不垂直但可能平行 |
| B、a和b可能垂直也可能平行 |
| C、a和b不平行但可能垂直 |
| D、a和b既不垂直也不平行 |
关于x的不等式x2-4ax+3a2＜0（a＞0）的解集为（x1，x2），则x1+x2+
的最小值是（ ）
| a |
| x1x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
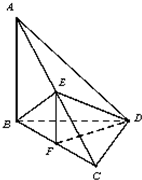如图，已知三棱锥A-BCD，AB⊥BD，AD⊥CD，E，F分别为AC，BC的中点，且△BEC为正三角形．