题目内容
利用秦九韶算法计算多项式f（x）=3x6+4x5+5x4+6x3+7x2+8x+1当x=4的值的时候需要做乘法和加法的次数分别为（ ）??
| A、6?6 | B、5?6 |
| C、5?5 | D、6?5 |
考点：秦九韶算法,中国古代数学瑰宝
专题：算法和程序框图
分析：利用“秦九韶算法”即可得出．
解答：
解：f（x）=3x6+4x5+5x4+6x3+7x2+8x+1
=（（（（（3x+4）x+5）x+6）x+7）x+8）x+1，
因此利用“秦九韶算法”计算多项式f（x）当x=4的值的时候需要做乘法和加法的次数分别是：6，6．
故选：A．
=（（（（（3x+4）x+5）x+6）x+7）x+8）x+1，
因此利用“秦九韶算法”计算多项式f（x）当x=4的值的时候需要做乘法和加法的次数分别是：6，6．
故选：A．
点评：本题考查了“秦九韶算法”的应用，属于基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设f（x）=x2-2x-4lnx，则f′（x）＜0的解集为（ ）
| A、（2，+∞） |
| B、（-1，0）U（2，+∞） |
| C、（-1，2） |
| D、（0，2） |
已知面α⊥β，α∩β=l，直线a?α，直线b?β，a，b与l斜交，则（ ）
| A、a和b不垂直但可能平行 |
| B、a和b可能垂直也可能平行 |
| C、a和b不平行但可能垂直 |
| D、a和b既不垂直也不平行 |
关于x的不等式x2-4ax+3a2＜0（a＞0）的解集为（x1，x2），则x1+x2+
的最小值是（ ）
| a |
| x1x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知椭圆
+
=1(a＞b＞0)左顶点C，A为椭圆在第一象限的点，直线OA交椭圆于另一点B，椭圆的左焦点为F1，若直线AF1交BC于M，且
=2
，则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| BM |
| MC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC内接于圆O（圆心是三边垂直平分线的交点），若
•
=2
•
，且|AB|=3，|CA|=6，则cosA的值是（ ）
| CO |
| AB |
| BO |
| CA |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
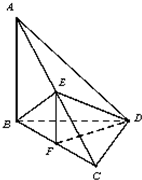如图，已知三棱锥A-BCD，AB⊥BD，AD⊥CD，E，F分别为AC，BC的中点，且△BEC为正三角形．
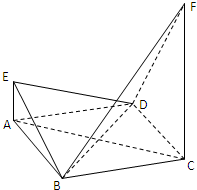已知四边形ABCD是菱形，其对角线AC=4，BD=2，直线AE，CF都与平面ABCD垂直，AE=1，CF=4．