题目内容
已知方程组
对此方程组的每一组正实数解(x,y,z,u),其中z≥y,都存在正实数M,且满足M≤
,则M的最大值是( )
|
| z |
| y |
| A、1 | ||
B、3+2
| ||
C、6+4
| ||
D、3-2
|
考点:基本不等式在最值问题中的应用
专题:综合题,不等式的解法及应用
分析:由题意,2y+z=x+2u≥2
=4
,可得2+
≥4
,令t=
,则t≥1,2+t2≥4t,解不等式可得t≥2+
,根据存在正实数M,且满足M≤
,即可得出结论.
| 2xu |
| yz |
| z |
| y |
|
|
| 2 |
| z |
| y |
解答:
解:由题意,2y+z=x+2u≥2
=4
,
∴2+
≥4
,
令t=
,则t≥1,2+t2≥4t,
∴t2-4t+2≥0,
∵t≥1,
∴t≥2+
,
∴
=t2≥6+4
,
∵存在正实数M,且满足M≤
,
∴M≤6+4
,
∴M的最大值是6+4
.
故选C.
| 2xu |
| yz |
∴2+
| z |
| y |
|
令t=
|
∴t2-4t+2≥0,
∵t≥1,
∴t≥2+
| 2 |
∴
| z |
| y |
| 2 |
∵存在正实数M,且满足M≤
| z |
| y |
∴M≤6+4
| 2 |
∴M的最大值是6+4
| 2 |
故选C.
点评:本题考查基本不等式的运用,考查学生分析解决问题的能力,正确运用基本不等式是关键.

练习册系列答案
相关题目
函数y=1-
sinx的单调区间是( )
| 2 |
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
关于x的不等式x2-4ax+3a2<0(a>0)的解集为(x1,x2),则x1+x2+
的最小值是( )
| a |
| x1x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若双曲线
-
=1(a>0,b>0)的右顶点为A,过其左焦点F作x轴的垂线交双曲线于M,N两点,且
•
>0,则该双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| MA |
| NA |
| A、(2,+∞) | ||
| B、(1,2) | ||
C、(
| ||
D、(1,
|
已知△ABC内接于圆O(圆心是三边垂直平分线的交点),若
•
=2
•
,且|AB|=3,|CA|=6,则cosA的值是( )
| CO |
| AB |
| BO |
| CA |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
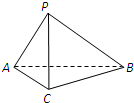 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.