题目内容
用二分法求出ln（2x+6）+2=3x 在区间（1，2）内的近似解（精确到0.1）．
考点：二分法求方程的近似解
专题：计算题,函数的性质及应用
分析：按照用二分法求函数零点近似值得步骤求解即可．注意验证精确度的要求．
解答：
令f（x）=ln（2x+6）-3x+2，
用计算器做出如下对应值表，
观察上表，可知零点在（1，2）内，
取区间中点x1=1.5，且f（1.5）≈-1，00，从而，可知零点在（1，1.5）内；
再取区间中点x2=1.25，且f（1.25）≈0.20，从而，可知零点在（1.25，1.5）内；
同理取区间中点x3=1.375，且f（1.375）＜0，从而，可知零点在（1.25，1.375）内；
由于区间（1.25，1.375）内任一值精确到0.1后都是1.3，
故ln（2x+6）+2=3x 在区间（1，2）内的近似解是1.3．
用计算器做出如下对应值表，
| x | -2 | -1 | 0 | 1 | 2 |
| f（x） | 2.5820 | 3.0530 | 2.7918 | 1.0794 | -4.6974 |
取区间中点x1=1.5，且f（1.5）≈-1，00，从而，可知零点在（1，1.5）内；
再取区间中点x2=1.25，且f（1.25）≈0.20，从而，可知零点在（1.25，1.5）内；
同理取区间中点x3=1.375，且f（1.375）＜0，从而，可知零点在（1.25，1.375）内；
由于区间（1.25，1.375）内任一值精确到0.1后都是1.3，
故ln（2x+6）+2=3x 在区间（1，2）内的近似解是1.3．
点评：本题考查用二分法求函数的近似零点的过程，每经过一次操作，区间长度变为原来的一半．要注意“精确度”与“精确到”的区别．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知函数f（x）=sin(2x-
)（x∈R），下面结论错误的是（ ）
| π |
| 3 |
| A、函数f（x）的最小正周期为π | ||
B、函数f（x）在区间[0，
| ||
| C、函数f（x）的图象关于直线x=0对称 | ||
D、函数f(x+
|
已知函数f（x）=sin（2ωx-
）（ω＞0）的最小正周期为π，则函数f（x）的图象的一条对称轴方程是（ ）
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
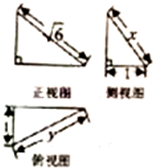
某几何体的三视图如图所示，则t=x-y的取值范围是（ ）
| A、[-4，4] | ||||
| B、（-1，1） | ||||
| C、[-1，1] | ||||
D、（1-
|
一个正三棱柱恰好有一个内切球（球与三棱柱的两个底面和三个侧面都相切）和一个外接球（球经过三棱柱的6个顶点），则此内切球与外接球表面积之比为（ ）
| A、1：3 | B、1：5 |
| C、1：7 | D、1：9 |