题目内容
已知函数f（x）=sin(2x-
)（x∈R），下面结论错误的是（ ）
| π |
| 3 |
| A、函数f（x）的最小正周期为π | ||
B、函数f（x）在区间[0，
| ||
| C、函数f（x）的图象关于直线x=0对称 | ||
D、函数f(x+
|
考点：正弦函数的图象
专题：计算题,三角函数的图像与性质
分析：求出的周期、奇偶性、单调区间，可得A、B、D都正确，C错误．
解答：
解：由周期公式可得：T=
=π，故A正确；
由2kπ-
≤2x-
≤2kπ+
可解得函数的单调递增区间为：[kπ-
，kπ+
]，k∈Z，故明显B正确；
由于f（0）=sin（-
）=-
，不是函数的最值，故C不正确；
由于f（x+
）=sin2x，有sin（-2x）=-sin2x，故D正确．
故选：C．
| 2π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
由于f（0）=sin（-
| π |
| 3 |
| ||
| 2 |
由于f（x+
| π |
| 6 |
故选：C．
点评：本题主要考查复合三角函数的周期性、奇偶性、单调性的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
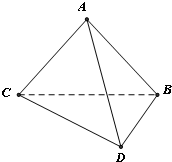如图，将一副三角板拼接，使他们有公共边BC，且使这两个三角形所在的平面互相垂直，∠BAC=∠CBD=90°，AB=AC，∠BCD=30°，BC=6．