题目内容
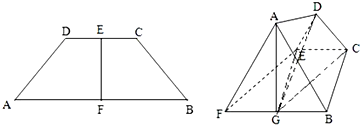
如图,已知平行六面体ABCD-A′B′C′D′,化简
+
-
.

| AC′ |
| D′B |
| DC |

考点:空间向量的基本定理及其意义
专题:空间向量及应用
分析:直接利用空间向量的演算法求解即可.
解答:
 解:平行六面体ABCD-A′B′C′D′,延长AB至AE,使得AB=BE,
解:平行六面体ABCD-A′B′C′D′,延长AB至AE,使得AB=BE,
=
,
=
,
∴
+
-
=2
-
=
.
故答案为:
.
 解:平行六面体ABCD-A′B′C′D′,延长AB至AE,使得AB=BE,
解:平行六面体ABCD-A′B′C′D′,延长AB至AE,使得AB=BE,| AB |
| DC |
| D′B |
| C′E |
∴
| AC′ |
| D′B |
| DC |
| AB |
| DC |
| AB |
故答案为:
| AB |
点评:本题考查空间向量的运算,考查计算能力以及作图能力.

练习册系列答案
相关题目
已知集合A={y|y=x2-2x+2,-1≤x≤2},B={x|
>1}},若任取x∈A,则x∈A∩B的概率为( )
| 2x-7 |
| x-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
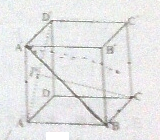
在正方体ABCD-A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是( )

A、0<θ<
| ||
B、0<θ≤
| ||
C、0≤θ≤
| ||
D、0<θ≤
|
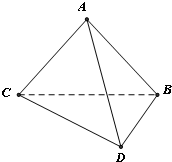 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.